| Railroad-Highway Grade Crossing Handbook - Revised Second Edition August 2007 | |
| Section 3: Assessment of Crossing Safety and Operation | Table of Contents | Previous | Next |
III
Assessment of Crossing Safety and Operation
The Federal Highway Administration (FHWA) requires each state to develop and implement a highway safety improvement program (HSIP) that consists of three components: planning, implementation, and evaluation. The process for improving safety and operations at highway-railroad grade crossings consists of the same three components and may be considered part of a state’s HSIP.
FHWA policy and procedures for an HSIP are contained in the Federal-Aid Policy Guide (FAPG) Title 23—Code of Federal Regulations (and Non-regulatory Supplements). The objective of an HSIP is to reduce “the number and severity of accidents” and decrease “the potential for accidents on all highways.” FAPG 924 requires the planning component to consist of:
• A process for collecting and maintaining a record of collision, traffic, and highway data, including, for highway-rail grade crossings, the characteristics of both highway and train traffic.
• A process for analyzing available data to identify highway locations, sections, and elements determined to be hazardous on the basis of collision experience or collision potential.
• A process for conducting engineering studies of hazardous locations, sections, and elements to develop highway safety improvement projects.
• A process for establishing priorities for implementing highway safety improvement projects.
The implementation component consists of a process for programming and implementing safety improvements. The evaluation component consists of a process for determining the effect that safety improvements have in reducing the number and severity of collisions and potential collisions.
This section of the Railroad-Highway Grade Crossing Handbook—Revised Second Edition provides guidance for the planning component, consisting of the collection and maintenance of data, the analysis of data, and engineering studies. In addition, the “systems approach,” a method by which several crossings are studied collectively, is discussed. Chapter IV identifies the various crossing improvements available. Chapter V presents guidelines for selecting improvements based on safety and operational effectiveness and costs. Chapter VI provides guidelines for the implementation component of the safety program, Chapter VII discusses maintenance programs, and Chapter VIII addresses the evaluation component.
A. Collection and Maintenance of Data
A systematic method for identifying problem locations is most important. For highway-railroad grade crossings, two types of information are needed: inventory and collision data. Inventory data include the location of the crossing, volumes of highway and train traffic over the crossing, and physical elements of the crossing. Collision data for each crossing are also needed.
1. U.S. Department of Transportation Grade Crossing Inventory
FAPG 924.9(a)(1) specifies that each state maintain “a process for collecting and maintaining a record of accident, traffic, and highway data, including, for railroad-highway grade crossings, the characteristics of both highway and train traffic.” State maintenance of the U.S. Department of Transportation (U.S. DOT) National Highway-Rail Crossing Inventory will satisfy this survey requirement. State inventories containing data similar to that provided in the national inventory will also suffice.
Figure 3. U.S. DOT Crossing Inventory Form
Download a PDF file of Figure 3: To view PDF files, you can use the Adobe® Reader®. |
The U.S. DOT National Highway-Rail Crossing Inventory was developed in the early 1970s through the cooperative efforts of FHWA, the Federal Railroad Administration (FRA), the Association of American Railroads (AAR), individual states, and individual railroads. Each crossing was surveyed—both public and private, grade separated and at grade—and data were recorded on the inventory form, as shown in Figure 3. The inventory contains data on the location of the crossing, the amount and type of highway and train traffic, traffic control devices, and other physical elements of the crossing.
Each crossing was assigned a unique identification number consisting of six numeric characters and an alphabetic character. The alphabetic character provides an algorithmic check of the six numeric characters. To determine the correct alphabetic character, sum the products of each of the first six digits times the digit’s position (position one is the left-most digit). Divide this total sum by 22 and then interpolate the remainder according to the following:
0 |
- |
A |
6 |
- |
G |
12 |
- |
N |
17 |
- |
U |
1 |
- |
B |
7 |
- |
H |
13 |
- |
P |
18 |
- |
V |
2 |
- |
C |
8 |
- |
J |
14 |
- |
R |
19 |
- |
W |
3 |
D |
9 |
K |
15 |
S |
20 |
X |
||||
4 |
- |
E |
10 |
- |
L |
16 |
- |
T |
21 |
- |
Y |
5 |
- |
F |
11 |
- |
M |
The crossing identification number, shown in Figure 4, was installed at each crossing by attaching a tag to a crossbuck post or flashing light post. The two most common methods used to install permanent tags at a crossing are a metal tag on which the crossing number is embossed by raised imprinting and stenciling the number on the post.
Figure 4. Crossing Identification Number Tag

Source: Railroad-Highway Grade Crossing Handbook, Second Edition. Washington, DC: U.S. Department of Transportation, Federal Highway Administration, 198
FRA serves as custodian of the national inventory file. Data in the inventory are kept current through the voluntary submission of information by the states and railroads. Because the national inventory is updated by numerous states and railroads, systematic and uniform procedures are required to assist FRA in processing the data. Two basic procedures have been developed.
Individual update forms. This is the procedure originally developed for updating the national inventory. Whenever a change occurs at a crossing, such as the installation of traffic control devices, the railroad or state initiates an update form. This involves completing the following identification data elements on the form: crossing identification number; effective date of the change; state; county; railroad; and type of update, such as a change at an existing crossing, a new crossing, or a closed crossing. Other data elements are completed only if they have changed or if they were not previously reported, such as for a new crossing.
To ensure that the state and railroad are in agreement on the elements contained in the inventory, a process was developed by which each would have the opportunity to review an update initiated by the other. If the railroad initiates the update, it retains a copy of the form and sends the original to the state agency. The state reviews the information and makes any appropriate changes. It then sends a copy back to the railroad for its files and sends the original to FRA for processing.
If a state initiates the update, it retains a copy and sends the original to the railroad for its review. The railroad retains a copy for its files and returns the original to the state. The state retains a copy and submits the original to FRA for processing.
This procedure allows both the state and the railroad to concur on the crossing information prior to submittal to FRA, and establishes the state as the agency that submits all data to FRA. Another advantage of this procedure is that both the state and the railroad have a hardcopy record of the update that can be placed in a file along with the original inventory record.
The primary disadvantage of the individual form method is that the form must be completed for every change. This may result in a time-consuming effort, particularly for changes that affect a number of crossings. For example, if a railroad changes its operation over a route that results in an increase in the number of trains per day, an individual form would be completed for each crossing. To assist in these types of changes, FRA has established procedures for the mass updating of one or two data elements.
Electronic updates.52 Another updating procedure involves the submission of data via computer electronic file. This method is advantageous for states and railroads that maintain the inventory on a computer. A state or railroad may enter changes onto its own computer file and then periodically send FRA a file of the changes in a prescribed format. This method, once established, provides for the updating of the national file with relative ease. However, three cautions should be noted:
• The information contained in electronic files must be in the prescribed format. Because FRA receives information from 50 states and numerous railroads, it must be able to process the files without having to make any changes to format. Details on the required format can be obtained from FRA’s Website.
• The electronic files should contain only changed information, not the entire crossing record. FRA’s procedures create a new crossing record whenever any data element is changed. The national inventory consists of 2 million original crossing records.
• The other party must be provided with a copy of the changed information for its records.
FRA can provide information from the national inventory in three primary ways.
• One page per crossing printout: This is simply a computer-generated printout that contains all the information for a crossing on a single 8.5-inch by 11-inch sheet of paper. The information has been decoded and is easy to read. It is obtained from the FRA Website.
• Continuous feed form: This is identical to the individual form update that can be generated by computer.
• Lists: FRA will also generate, upon request, a list of specified information for specified crossings. This might be useful for obtaining current data on the elements contained in a priority index formula.
Data contained in the national inventory or a state inventory must be used with care. The data should be verified in the field, as discussed in a later section on engineering studies. The national inventory is used not only by states and railroads in conducting their crossing improvement programs but also by national and federal agencies in assessing crossing improvement needs and conducting research. Both states and railroads are urged to keep the information in this valuable database up to date.
2. Grade Crossing Collision Data
Information on highway-rail grade crossing collisions is also needed to assess safety and operations. Data on collisions involving trains are essential in identifying crossings with safety problems. In addition, data on collisions not involving trains but occurring at or near a crossing are useful. For example, non-train-involved collisions may indicate a deficiency in stopping sight distance such that a vehicle suddenly stops at a crossing, causing the following vehicle to hit the leading vehicle in the rear.
Collision data are available from several sources, including state and local police and FRA. In addition, the National Highway Transportation Safety Administration (NHTSA) and FHWA maintain some information on crossing collisions.
Most state and local police maintain a record of all highway traffic collisions, including those occurring at or near crossings. It is essential that the police record the crossing identification number on the police accident report form. If the collision did not involve a train but occurred at or near a crossing, the crossing identification number should also be recorded on the police report form. Thus, collisions in which the presence of the crossing (regardless of the presence of a train) was a contributing factor to the collision can be identified. It is recommended that the police accident report form give the crossing identification number for collisions that occur within 200 feet of a crossing.
FRA requires each railroad to report any “impact between railroad on-track equipment and an automobile, bus, truck, motorcycle, bicycle, farm vehicle, or pedestrian at a rail-highway grade crossing.”53 The form used for the railroad to report highway-rail crossing collisions is shown in Figure 5. FRA prepares an annual summary of the collision data (and the national inventory data) entitled “Railroad Safety Statistics Annual Report.” This document and other data contained in the collision data file can be obtained from FRA’s Website.
NHTSA maintains a database on all fatal highway traffic collisions, including those occurring at highway-rail grade crossings. The Fatal Accident Reporting System (FARS) database can be accessed at www-fars. nhtsa.dot.gov.
The Federal Motor Carrier Safety Administration (FMCSA) maintains data on highway collisions involving motor carriers. A recordable collision is “an occurrence involving a commercial motor vehicle operating on a highway in engaged in interstate or intrastate commerce which results in (i) a fatality; (ii) Bodily injury to a person who, as a result of the injury, immediately receives medical treatment away from the scene of the accident; or, (iii) One or more motor vehicles incurring disabling damage as a result of the accident, requiring the motor vehicle(s) to be transported away from the scene by a tow truck or other motor vehicle.”54
Figure 5. Accident Report Form for Federal Railroad Administration
Download a PDF file of Figure 5: To view PDF files, you can use the Adobe® Reader®. |
In the past, FMCSA required motor carriers to report crashes directly to the agency. This is no longer the case. This information is now forwarded by states. However, motor carriers must maintain accident registers for three years after the date of each accident occurring on or after April 29, 2003 (49 CFR 390.15). (Previously, the register had to be maintained for one year.) An example of a comprehensive state crash reporting form is included in Appendix C.
Collisions involving the transport of hazardous materials are reported to the Materials Transportation Bureau (MTB) of the Research and Special Programs Administration. An immediate telephone notice is required under certain conditions, and a detailed written report is required whenever there is any unintentional release of a hazardous material during transportation or temporary storage related to transportation. Collisions are to be reported when, as a direct result of hazardous materials: a person is killed; a person receives injuries requiring hospitalization; estimated carrier or other property damage exceeds $50,000; or a situation exists such that a continuing danger to life exists at the scene of the incident. The form used for reporting these collisions to MTB is shown in Appendix D.
Significant transportation accidents are investigated by the National Transportation Safety Board (NTSB). NTSB issues a report for each accident investigated. The report presents the circumstances of the accident, the data collected, and the analysis of the data as well as conclusions, which are identified as “findings” of NTSB. In addition, NTSB issues specific recommendations to various parties for improvement of safety conditions. Appendix E provides summaries of a number of selected key grade crossing collision investigations provided by NTSB.
B. Hazard Indices and Accident Prediction Formulae
A systematic method for identifying crossings that have the most need for safety and/or operational improvements is essential to comply with requirements of the FAPG, which specifies that each state should maintain a priority schedule of crossing improvements. The priority schedule is to be based on:
• The potential reduction in the number and/or severity of collisions.
• The cost of the projects and the resources available.
• The relative hazard of public highway-rail grade crossings based on a hazard index formula.
• On-site inspections of public crossings.
• The potential danger to large numbers of people at public crossings used on a regular basis by passenger trains, school buses, transit buses, pedestrians, bicyclists, or by trains and/ or motor vehicle carrying hazardous materials.
• Other criteria as appropriate in each state.
Various hazard indices and collision prediction formulae have been developed for ranking highway-rail grade crossings. These are commonly used to identify crossings to be investigated in the field. Procedures for conducting the on-site inspection are discussed in the next section. Some hazard indices incorporate collision history as a factor in the ranking formula; if not, this factor should be subjectively considered.
1. Hazard Index
A hazard index ranks crossings in relative terms (the higher the calculated index, the more hazardous the crossing), whereas the collision prediction formulae are intended to compute the actual collision occurrence frequency at the crossing. A commonly used index is the New Hampshire Hazard Index ranking methodology (presented in Appendix F).
There are several advantages of using a hazard index to rank crossings. A mathematical hazard index enhances objectivity. It can be calculated by computer, facilitating the ranking process. As crossing conditions change, a computerized database can be updated and the hazard index recalculated.
In general, crossings that rank highest on the hazard index are selected to be investigated in the field by a diagnostic team, as discussed in the next section. Other crossings may be selected for a field investigation because they are utilized by buses, passenger trains, and vehicles transporting hazardous materials. FAPG requires that the potential danger to large numbers of people at crossings used on a regular basis by passenger trains, school buses, transit buses, pedestrians, bicyclists, or by trains and/or motor vehicles carrying hazardous materials be one of the considerations in establishing a priority schedule. Some states incorporate these considerations into a hazard index, thus providing an objective means of assessing the potential danger to large numbers of people.
Some states, however, consider these factors subjectively when selecting the improvement projects among the crossings ranked highest by the hazard index. Other states utilize a point system so that crossings high on the hazard index receive a specified number of points, as do crossings with a specified number of buses, passenger trains, and vehicles transporting hazardous materials.
Other states utilize the systems approach, considering all crossings within a specified system, such as all crossings along a passenger train corridor.
Crossings may also be selected for field investigation as a result of requests or complaints from the public. State district offices, local governmental agencies, other state agencies, and railroads may also request that a crossing be investigated for improvement. A change in highway or railroad operations over a crossing may justify the consideration of that crossing for improvement. For example, a new residential or commercial development may substantially increase the volume of highway traffic over a crossing such that its hazard index would greatly increase.
2. U.S. Department of Transportation Accident Prediction Model
A prediction model is intended to predict, in absolute terms, the likelihood of a collision occurring over a given period of time given conditions at the crossing. The following discussion presents the accident prediction model developed by U.S. DOT. (Other formulae are presented in Appendix F. ) Thus, an accident prediction model can also be used to either rank crossings or identify potential high-accident locations for further review.
The U.S. DOT collision prediction formula combines three independent calculations to produce a collision prediction value. The basic formula provides an initial hazard ranking based on a crossing’s characteristics, similar to other formulae such as the Peabody-Dimmick formula and the New Hampshire Index. The second calculation utilizes the actual collision history at a crossing over a determined number of years to produce a collision prediction value. This procedure assumes that future collisions per year at a crossing will be the same as the average historical collision rate over the time period used in the calculation. The third equation adds a normalizing constant, which is adjusted periodically to keep the procedure matched with current collision trends.
FRA has provided a Website where highway-rail intersection safety specialists may calculate the predicted collisions for any public highway-rail intersection in the national inventory.55
The basic collision prediction formula can be expressed as a series of factors that, when multiplied together, yield an initial predicted number of collisions per year at a crossing. Each factor in the formula represents a characteristic of the crossing described in the national inventory. The general expression of the basic formula is shown below:
a=K x El x MT x DT x HP x MS x HT x HL (1)
where:
a = initial collision prediction, collisions per year at the crossing
K = formula constant
EI = factor for exposure index based on product of highway and train traffic
MT = factor for number of main tracks
DT = factor for number of through trains per day during daylight
HP = factor for highway paved (yes or no)
MS = factor for maximum timetable speed
HT = factor for highway type
HL = factor for number of highway lanes
Different sets of equations are used for each of the three categories of traffic control devices: passive, flashing lights, and automatic gates, as shown in Table 16.
The structure of the basic collision prediction formula makes it possible to construct tables of numerical values for each factor. To predict the collisions at a particular crossing whose characteristics are known, the values of the factors are found in the table and multiplied together. The factor values for the three traffic control device categories are found in Tables 17, 18, and 19, respectively.
Table 16. U.S. DOT Collision Prediction Equations for Crossing Characteristic Factors
General Form of Basic Accident Prediction Formula: e = K x El x MT x DT x HP x MS x HT x HL
Crossing Characteristic Factors

c |
= annual average number of highway vehicles per day (total both directions) |
t |
= average total train movements per day |
mt |
= number of main tracks |
d |
= average number of thru trains per day during daylight |
hp |
= highway paved, yes = 1.0, no = 2.0 |
ms |
= maximum timetable speed, mph |
ht |
= highway type factor value |
hl |
= number of highway lanes |
Highway Type Rural |
Inventory Code |
ht Value |
Interstate |
01 |
I |
Other principal arterial |
02 |
2 |
Minor arterial |
06 |
3 |
Major collector |
07 |
4 |
Minor collector |
08 |
5 |
Local |
09 |
6 |
Urban |
||
Interstate |
11 |
1 |
Other freeway and expressway |
12 |
2 |
Other principal arterial |
14 |
3 |
Minor arterial |
16 |
4 |
Collector |
17 |
5 |
Local |
19 |
6 |
Source: Railroad-Highway Grade Crossing Handbook, Second Edition. Washington, DC: U.S. Department of Transportation, Federal Highway Administration, 1986.
The final collision prediction formula can be expressed as follows:
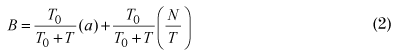
where:
B = second collision prediction, collisions per year at the crossing
a = initial collision prediction from basic formula, collisions per year at the crossing
N/T = collision history prediction, collisions per year, where N is the number of observed collisions in T years at the crossing
Values for the second collision prediction, B; for different values of the initial prediction, a; and different prior collision rates, N/T, are tabularized in Table 20, 21, 22, 23, and 24. Each table represents results for a specific number of years for which collision history data are available. If the number of years of collision data, T, is a fraction, the second collision prediction, B, can be interpolated from the tables or determined directly from the formula.
The formula provides the most accurate results if all the collision history available is used; however, the extent of improvement is minimal if data for more than five years are used. Collision history information older than five years may be misleading because of changes that occur to crossing characteristics over time. If a significant change has occurred to a crossing during the most recent five years, such as the installation of signals, only the collision data since that change should be used.
The final collision prediction, A, is developed by applying a normalizing constant to keep the procedure matched with current collision trends. The final formula, using constants established for 2003, is shown on page 60. (As of November 2003, these new constants will be in the Personal Computer Accident Prediction System software and an Internet version of the Highway-Rail Crossing Web Accident Prediction System located on the FRA Website.56)
Table 17. U.S. DOT Accident Prediction Factor Values for Crossings with Passive Warning Devices
K |
“c” x “t” |
EI |
Main |
MT |
Day Thru |
DT |
Highway Paved |
HP |
Maximum Timetable |
MS |
Highway Type |
HT |
Highway Lanes |
HL |
||||
0* |
1.00 |
0 |
1.00 |
0 |
1.00 |
1 (yes) |
1.00 |
0 |
1.00 |
01&11 |
1.00 |
1 |
1.00 |
|||||
1 |
- |
5 |
2.22 |
1 |
1.23 |
1 |
1.27 |
2 (no) |
0.54 |
5 |
1.04 |
02&12 |
0.90 |
2 |
1.00 |
|||
6 |
- |
10 |
3.30 |
2 |
1.52 |
2 |
1.38 |
10 |
1.08 |
06&14 |
0.82 |
3 |
1.00 |
|||||
11 |
- |
20 |
4.24 |
3 |
1.87 |
3 |
1.45 |
15 |
1.12 |
07&16 |
0.74 |
4 |
1.00 |
|||||
21 |
- |
30 |
5.01 |
4 |
2.31 |
4 |
1.50 |
20 |
1.17 |
08&17 |
0.67 |
5 |
1.00 |
|||||
31 |
- |
50 |
5.86 |
5 |
2.85 |
5 |
1.55 |
25 |
1.21 |
09&19 |
0.61 |
6 |
1.00 |
|||||
51 |
- |
80 |
6.89 |
6 |
3.51 |
6 |
1.58 |
30 |
1.26 |
7 |
1.00 |
|||||||
81 |
- |
120 |
7.95 |
7 |
1.61 |
35 |
1.31 |
8 |
1.00 |
|||||||||
121 |
- |
200 |
9.29 |
8 |
1.64 |
40 |
1.36 |
9 |
1.00 |
|||||||||
201 |
- |
300 |
10.78 |
9 |
1.67 |
45 |
1.41 |
|||||||||||
301 |
- |
400 |
12.06 |
10 |
1.69 |
50 |
1.47 |
|||||||||||
401 |
- |
500 |
13.11 |
11-20 |
1.78 |
55 |
1.53 |
|||||||||||
501 |
- |
600 |
14.02 |
21-30 |
1.91 |
60 |
1.59 |
|||||||||||
601 |
- |
700 |
14.82 |
31-40 |
2.00 |
65 |
1.65 |
|||||||||||
701 |
- |
1000 |
16.21 |
41-60 |
2.09 |
70 |
1.71 |
|||||||||||
1001 |
- |
1300 |
17.93 |
75 |
1.78 |
|||||||||||||
1301 |
- |
1600 |
19.37 |
80 |
1.85 |
|||||||||||||
1601 |
- |
2000 |
20.81 |
85 |
1.92 |
|||||||||||||
2001 |
- |
2500 |
22.42 |
90 |
2.00 |
|||||||||||||
2501 3001 |
-- |
3000 4000 |
23.97 25.98 |
General Form of Basic Accident Prediction Formula: a = K x El x MT x DT x HP x HT x HL |
||||||||||||||
4001 |
- |
6000 |
29.26 |
“c” x “t” = Number of highway vehicles per day, “c”, multiplied by total train movements per day, “t” El = Exposure index factor MT = Main tracks factor DT = Day thru trains factor HP = Highway paved factor MS =Maximum timetable speed factor HT = Highway type factor HL = Highway lanes factor * Less than one train per day ** See Table 16 for definition of highway type codes Source: Railroad-Highway Grade Crossing Handbook, Second Edition. Washington, DC: U.S. Department of Transportation, Federal Highway Administration, 1986.
|
||||||||||||||
6001 |
- |
8000 |
32.73 |
|||||||||||||||
8001 |
- |
10000 |
35.59 |
|||||||||||||||
10001 |
- |
15000 |
39.71 |
|||||||||||||||
15001 |
- |
20000 |
44.43 |
|||||||||||||||
20001 |
- |
25000 |
48.31 |
|||||||||||||||
25001 |
- |
30000 |
51.65 |
|||||||||||||||
30001 |
- |
40000 |
55.98 |
|||||||||||||||
40001 |
- |
50000 |
60.87 |
|||||||||||||||
50001 |
- |
60000 |
65.08 |
|||||||||||||||
60001 |
- |
70000 |
68.81 |
|||||||||||||||
70001 |
- |
90000 |
73.74 |
|||||||||||||||
90001 |
- |
79.44 |
||||||||||||||||
110001 |
- |
84.42 |
||||||||||||||||
130001 |
- |
91.94 |
||||||||||||||||
180001 |
- |
100.92 |
||||||||||||||||
230001 |
- |
109.94 |
||||||||||||||||
300001 |
- |
118.87 |
||||||||||||||||
Table 18. U.S. DOT Accident Prediction Factor Values for Crossings with Flashing Light Warning Devices
K |
“c” x “t” |
Main |
MT |
Day Thru |
DT |
Highway Paved |
HP |
Maximum Timetable |
MS |
Highway Type |
HT |
Highway Lanes |
HL |
||||
0* |
1.00 |
0 |
1.00 |
0 |
1.00 |
1 (yes) |
1.00 |
0 |
1.00 |
01&11 |
1.00 |
1 |
1.00 |
||||
1 |
- |
5 |
2.27 |
1 |
1.11 |
1 |
1.09 |
2 (no) |
1.00 |
5 |
1.00 |
02&12 |
1.00 |
2 |
1.15 |
||
6 |
- |
10 |
2.99 |
2 |
1.24 |
2 |
1.12 |
10 |
1.00 |
06&14 |
1.00 |
3 |
1.32 |
||||
11 |
- |
20 |
3.59 |
3 |
1.39 |
3 |
1.14 |
15 |
1.00 |
07&16 |
1.00 |
4 |
1.51 |
||||
21 |
- |
30 |
4.17 |
4 |
1.55 |
4 |
1.15 |
20 |
1.00 |
08&17 |
1.00 |
5 |
1.74 |
||||
31 |
- |
50 |
4.79 |
5 |
1.72 |
5 |
1.17 |
25 |
1.00 |
09&19 |
1.00 |
6 |
1.99 |
||||
51 |
- |
80 |
5.52 |
6 |
1.92 |
6 |
1.18 |
30 |
1.00 |
7 |
2.29 |
||||||
81 |
- |
120 |
6.27 |
7 |
1.18 |
35 |
1.00 |
8 |
2.63 |
||||||||
121 |
- |
200 |
7.20 |
8 |
1.19 |
40 |
1.00 |
9 |
3.02 |
||||||||
201 |
- |
300 |
8.22 |
9 |
1.20 |
45 |
1.00 |
||||||||||
301 |
- |
400 |
9.07 |
10 |
1.20 |
50 |
1.00 |
||||||||||
401 |
- |
500 |
9.77 |
11-20 |
1.23 |
55 |
1.00 |
||||||||||
501 |
- |
600 |
10.37 |
21-30 |
1.26 |
60 |
1.00 |
||||||||||
601 |
- |
700 |
10.89 |
31-40 |
1.28 |
65 |
1.00 |
||||||||||
701 |
- |
1000 |
11.79 |
41-60 |
1.30 |
70 |
1.00 |
||||||||||
1001 |
- |
1300 |
12.89 |
75 |
1.00 |
||||||||||||
1301 |
- |
1600 |
13.80 |
80 |
1.00 |
||||||||||||
1601 |
- |
2000 |
14.71 |
85 |
1.00 |
||||||||||||
2001 |
- |
2500 |
15.72 |
90 |
1.00 |
||||||||||||
3001 |
- |
4000 |
17.91 |
General Form of Basic Accident Prediction Formula: a = K x El x MT x DT x HP x HT x HL “c” x “t” = Number of highway vehicles per day, “c”, multiplied by total train movements per day, “t” El = Exposure index factor MT = Main tracks factor DT = Day thru trains factor HP = Highway paved factor MS =Maximum timetable speed factor HT = Highway type factor HL = Highway lanes factor * Less than one train per day ** See Table 16 for definition of highway type codes Source: Railroad-Highway Grade Crossing Handbook, Second Edition. Washington, DC: U.S. Department of Transportation, Federal Highway Administration, 1986.
|
|||||||||||||
4001 |
- |
6000 |
19.89 |
||||||||||||||
6001 |
- |
8000 |
21.97 |
||||||||||||||
8001 |
- |
10000 |
23.66 |
||||||||||||||
10001 |
- |
15000 |
26.08 |
||||||||||||||
15001 |
- |
20000 |
28.80 |
||||||||||||||
20001 |
- |
25000 |
31.02 |
||||||||||||||
25001 |
- |
30000 |
32.91 |
||||||||||||||
30001 |
- |
40000 |
35.34 |
||||||||||||||
40001 |
- |
50000 |
38.06 |
||||||||||||||
50001 |
- |
60000 |
40.39 |
||||||||||||||
60001 |
- |
70000 |
42.43 |
||||||||||||||
70001 |
- |
90000 |
45.11 |
||||||||||||||
90001 |
- |
48.18 |
|||||||||||||||
110001 |
- |
50.85 |
|||||||||||||||
130001 |
- |
54.84 |
|||||||||||||||
180001 |
- |
59.56 |
|||||||||||||||
230001 |
- |
64.25 |
|||||||||||||||
300001 |
- |
68.86 |
|||||||||||||||
Table 19. U.S. DOT Accident Prediction Factor Values for Crossings with Gate Warning Devices
K |
“c” x “t” |
EI |
Main Tracks |
MT |
Day Thru Trains |
DT |
Highway Paved |
HP |
Maximum |
MS |
Highway Type Code** |
HT |
Highway Lanes |
HL |
||||
0* |
1.00 |
0 |
1.00 |
0 |
1.00 |
1 (yes) |
1.00 |
0 |
1.00 |
01&11 |
1.00 |
1 |
1.00 |
|||||
1 |
- |
5 |
2.37 |
1 |
1.34 |
1 |
1.00 |
2 (no) |
1.00 |
5 |
1.00 |
02&12 |
1.00 |
2 |
1.11 |
|||
6 |
- |
10 |
3.18 |
2 |
1.79 |
2 |
1.00 |
10 |
1.00 |
06&14 |
1.00 |
3 |
1.23 |
|||||
11 |
- |
20 |
3.86 |
3 |
2.40 |
3 |
1.00 |
15 |
1.00 |
07&16 |
1.00 |
4 |
1.36 |
|||||
21 |
- |
30 |
4.51 |
4 |
3.21 |
4 |
1.00 |
20 |
1.00 |
08&17 |
1.00 |
5 |
1.51 |
|||||
31 |
- |
50 |
5.22 |
5 |
4.29 |
5 |
1.00 |
25 |
1.00 |
09&19 |
1.00 |
6 |
1.68 |
|||||
51 |
- |
80 |
6.07 |
6 |
5.74 |
6 |
1.00 |
30 |
1.00 |
7 |
1.86 |
|||||||
81 |
- |
120 |
6.94 |
7 |
1.00 |
35 |
1.00 |
8 |
2.07 |
|||||||||
121 |
- |
200 |
8.03 |
8 |
1.00 |
40 |
1.00 |
9 |
2.29 |
|||||||||
201 |
- |
300 |
9.23 |
9 |
1.00 |
45 |
1.00 |
|||||||||||
301 |
- |
400 |
10.25 |
10 |
1.00 |
50 |
1.00 |
|||||||||||
401 |
- |
500 |
11.08 |
11-20 |
1.00 |
55 |
1.00 |
|||||||||||
501 |
- |
600 |
11.80 |
21-30 |
1.00 |
60 |
1.00 |
|||||||||||
601 |
- |
700 |
12.43 |
31-40 |
1.00 |
65 |
1.00 |
|||||||||||
701 |
- |
1000 |
13.51 |
41-60 |
1.00 |
70 |
1.00 |
|||||||||||
1001 |
- |
1300 |
14.84 |
75 |
1.00 |
|||||||||||||
1301 |
- |
1600 |
15.96 |
80 |
1.00 |
|||||||||||||
1601 |
- |
2000 |
17.07 |
85 |
1.00 |
|||||||||||||
2001 |
- |
2500 |
18.30 |
90 |
1.00 |
|||||||||||||
3001 |
- |
4000 |
21.00 |
General Form of Basic Accident Prediction Formula: a = K x El x MT x DT x HP x HT x HL “c” x “t” = Number of highway vehicles per day, “c”, multiplied by total train movements per day, “t” El = Exposure index factor MT = Main tracks factor DT = Day thru trains factor HP = Highway paved factor MS =Maximum timetable speed factor HT = Highway type factor HL = Highway lanes factor * Less than one train per day ** See Table 16 for definition of highway type codes Source: Railroad-Highway Grade Crossing Handbook, Second Edition. Washington, DC: U.S. Department of Transportation, Federal Highway Administration, 1986.
|
||||||||||||||
4001 |
- |
6000 |
23.46 |
|||||||||||||||
6001 |
- |
8000 |
26.06 |
|||||||||||||||
8001 |
- |
10000 |
28.18 |
|||||||||||||||
10001 |
- |
15000 |
||||||||||||||||
15001 |
- |
20000 |
34.67 |
|||||||||||||||
20001 |
- |
25000 |
37.49 |
|||||||||||||||
25001 |
- |
30000 |
39.91 |
|||||||||||||||
30001 |
- |
40000 |
43.03 |
|||||||||||||||
40001 |
- |
50000 |
46.53 |
|||||||||||||||
50001 |
- |
60000 |
49.53 |
|||||||||||||||
60001 |
- |
70000 |
52.18 |
|||||||||||||||
70001 |
- |
90000 |
55.67 |
|||||||||||||||
90001 |
- |
59.68 |
||||||||||||||||
110001 |
- |
63.16 |
||||||||||||||||
130001 |
- |
68.41 |
||||||||||||||||
180001 |
- |
74.63 |
||||||||||||||||
230001 |
- |
80.85 |
||||||||||||||||
300001 |
- |
86.98 |
||||||||||||||||
| .6500 passive devices | |
| A = | .5001 flashing lights |
| .5725 gates |
Accident severity. Additional equations within the U.S. DOT model are used to predict the likelihood of fatalities and injuries. The probability of a fatal accident given an accident, P(FA|A), is expressed as:
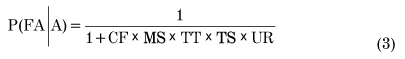
where:
CF = formula constant = 695
MS = factor for maximum timetable train speed
TT = factor for through trains per day
TS = factor for switch trains per day
UR = factor for urban or rural crossing
Table 20. U.S. DOT Final Accident Prediction from Initial Prediction and Accident History (1 year of accident data (T = 1))
Initial Prediction from Basic Model, a |
Number of Accidents, N, in T Years |
|||||
0 |
1 |
2 |
3 |
4 |
5 |
|
0.00 |
0.000 |
0.048 |
0.095 |
0.143 |
0.190 |
0.238 |
0.01 |
0.009 |
0.066 |
0.123 |
0.179 |
0.236 |
0.292 |
0.02 |
0.019 |
0.084 |
0.150 |
0.215 |
0.280 |
0.346 |
0.03 |
0.028 |
0.102 |
0.176 |
0.250 |
0.324 |
0.398 |
0.04 |
0.037 |
0.119 |
0.202 |
0.284 |
0.367 |
0.450 |
0.05 |
0.045 |
0.136 |
0.227 |
0.318 |
0.409 |
0.500 |
0.06 |
0.054 |
0.153 |
0.252 |
0.351 |
0.450 |
0.550 |
0.07 |
0.063 |
0.170 |
0.277 |
0.384 |
0.491 |
0.598 |
0.08 |
0.071 |
0.186 |
0.301 |
0.416 |
0.531 |
0.646 |
0.09 |
0.079 |
0.202 |
0.325 |
0.447 |
0.570 |
0.693 |
0.10 |
0.087 |
0.217 |
0.348 |
0.478 |
0.609 |
0.739 |
0.20 |
0.160 |
0.360 |
0.560 |
0.760 |
0.960 |
1.160 |
0.30 |
0.222 |
0.481 |
0.741 |
1.000 |
1.259 |
1.519 |
0.40 |
0.276 |
0.586 |
0.897 |
1.207 |
1.517 |
1.828 |
0.50 |
0.323 |
0.677 |
1.032 |
1.387 |
1.742 |
2.097 |
0.60 |
0.364 |
0.758 |
1.152 |
1.545 |
1.939 |
2.333 |
0.70 |
0.400 |
0.829 |
1.257 |
1.686 |
2.114 |
2.543 |
0.80 |
0.432 |
0.892 |
1.351 |
1.811 |
2.270 |
2.730 |
0.90 |
0.462 |
0.949 |
1.436 |
1.923 |
2.410 |
2.897 |
1.00 |
0.488 |
1.000 |
1.512 |
2.024 |
2.537 |
3.049 |
1.10 |
0.512 |
1.047 |
1.581 |
2.116 |
2.651 |
3.186 |
1.20 |
0.533 |
1.089 |
1.644 |
2.200 |
2.756 |
3.311 |
1.30 |
0.553 |
1.128 |
1.702 |
2.277 |
2.851 |
3.426 |
1.40 |
0.571 |
1.163 |
1.755 |
2.347 |
2.939 |
3.531 |
1.50 |
0.588 |
1.196 |
1.804 |
2.412 |
3.020 |
3.627 |
1.60 |
0.604 |
1.226 |
1.849 |
2.472 |
3.094 |
3.717 |
1.70 |
0.618 |
1.255 |
1.891 |
2.527 |
3.164 |
3.800 |
1.80 |
0.632 |
1.281 |
1.930 |
2.579 |
3.228 |
3.877 |
1.90 |
0.644 |
1.305 |
1.966 |
2.627 |
3.288 |
3.949 |
2.00 |
0.656 |
1.328 |
2.000 |
2.672 |
3.344 |
4.016 |
2.10 |
0.667 |
1.349 |
2.032 |
2.714 |
3.397 |
4.079 |
2.20 |
0.677 |
1.369 |
2.062 |
2.754 |
3.446 |
4.138 |
2.30 |
0.687 |
1.388 |
2.090 |
2.791 |
3.493 |
4.194 |
2.40 |
0.696 |
1.406 |
2.116 |
2.826 |
3.536 |
4.246 |
2.50 |
0.704 |
1.423 |
2.141 |
2.659 |
3.577 |
4.296 |
Source: Railroad-Highway Grade Crossing Handbook, Second Edition. Washington, DC: U.S. Department of Transportation, Federal Highway Administration, 1986. |
||||||
Table 21. U.S. DOT Final Accident Prediction from Initial Prediction and Accident History
(2 years of accident data (T = 2))
Initial Prediction from Basic Model, a |
Number of Accidents, N, in T Years |
||||||||
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
0.00 |
0.000 |
0.045 |
0.091 |
0.136 |
0.182 |
0.227 |
0.273 |
0.318 |
0.364 |
0.01 |
0.009 |
0.063 |
0.116 |
0.170 |
0.223 |
0.277 |
0.330 |
0.384 |
0.438 |
0.02 |
0.018 |
0.079 |
0.140 |
0.202 |
0.263 |
0.325 |
0.386 |
0.447 |
0.509 |
0.03 |
0.026 |
0.095 |
0.164 |
0.233 |
0.302 |
0.371 |
0.440 |
0.509 |
0.578 |
0.04 |
0.034 |
0.110 |
0.186 |
0.263 |
0.339 |
0.415 |
0.492 |
0.568 |
0.644 |
0.05 |
0.042 |
0.125 |
0.208 |
0.292 |
0.375 |
0.458 |
0.542 |
0.625 |
0.708 |
0.06 |
0.049 |
0.139 |
0.230 |
0.320 |
0.410 |
0.500 |
0.590 |
0.680 |
0.770 |
0.07 |
0.056 |
0.153 |
0.250 |
0.347 |
0.444 |
0.540 |
0.637 |
0.734 |
0.831 |
0.08 |
0.063 |
0.167 |
0.270 |
0.373 |
0.476 |
0.579 |
0.683 |
0.786 |
0.889 |
0.09 |
0.070 |
0.180 |
0.289 |
0.398 |
0.508 |
0.617 |
0.727 |
0.836 |
0.945 |
0.10 |
0.077 |
0.192 |
0.308 |
0.423 |
0.538 |
0.654 |
0.769 |
0.885 |
1.000 |
0.20 |
0.133 |
0.300 |
0.467 |
0.633 |
0.800 |
0.967 |
1.133 |
1.300 |
1.467 |
0.30 |
0.176 |
0.382 |
0.588 |
0.794 |
1.000 |
1.206 |
1.412 |
1.618 |
1.824 |
0.40 |
0.211 |
0.447 |
0.684 |
0.921 |
1.158 |
1.395 |
1.632 |
1.868 |
2.105 |
0.50 |
0.238 |
0.500 |
0.762 |
1.024 |
1.286 |
1.548 |
1.810 |
2.071 |
2.333 |
0.60 |
0.261 |
0.543 |
0.826 |
1.109 |
1.391 |
1.674 |
1.957 |
2.239 |
2.522 |
0.70 |
0.280 |
0.580 |
0.880 |
1.180 |
1.480 |
1.780 |
2.080 |
2.380 |
2.680 |
0.80 |
0.296 |
0.611 |
0.926 |
1.241 |
1.556 |
1.870 |
2.185 |
2.500 |
2.815 |
0.90 |
0.310 |
0.638 |
0.966 |
1.293 |
1.621 |
1.948 |
2.276 |
2.603 |
2.931 |
1.00 |
0.323 |
0.661 |
1.000 |
1.339 |
1.677 |
2.016 |
2.355 |
2.694 |
3.032 |
1.10 |
0.333 |
0.682 |
1.030 |
1.379 |
1.727 |
2.076 |
2.424 |
2.773 |
3.121 |
1.20 |
0.343 |
0.700 |
1.057 |
1.414 |
1.771 |
2.129 |
2.486 |
2.843 |
3.200 |
1.30 |
0.351 |
0.716 |
1.081 |
1.446 |
1.811 |
2.176 |
2.541 |
2.905 |
3.270 |
1.40 |
0.359 |
0.731 |
1.103 |
1.474 |
1.846 |
2.218 |
2.590 |
2.962 |
3.333 |
1.50 |
0.366 |
0.744 |
1.122 |
1.500 |
1.878 |
2.256 |
2.634 |
3.012 |
3.390 |
1.60 |
0.372 |
0.756 |
1.140 |
1.523 |
1.907 |
2.291 |
2.674 |
3.058 |
3.442 |
1.70 |
0.378 |
0.767 |
1.156 |
1.544 |
1.933 |
2.322 |
2.711 |
3.100 |
3.489 |
1.80 |
0.383 |
0.777 |
1.170 |
1.564 |
1.957 |
2.351 |
2.745 |
3.138 |
3.532 |
1.90 |
0.388 |
0.786 |
1.184 |
1.582 |
1.980 |
2.378 |
2.776 |
3.173 |
3.571 |
2.00 |
0.392 |
0.794 |
1.196 |
1.598 |
2.000 |
2.402 |
2.804 |
3.206 |
3.608 |
2.10 |
0.396 |
0.802 |
1.208 |
1.613 |
2.019 |
2.425 |
2.830 |
3.236 |
3.642 |
2.20 |
0.400 |
0.809 |
1.218 |
1.627 |
2.036 |
2.445 |
2.855 |
3.264 |
3.673 |
2.30 |
0.404 |
0.816 |
1.228 |
1.640 |
2.053 |
2.465 |
2.877 |
3.289 |
3.702 |
2.40 |
0.407 |
0.822 |
1.237 |
1.653 |
2.068 |
2.483 |
2.898 |
3.314 |
3.729 |
2.50 |
0.410 |
0.828 |
1.246 |
1.664 |
2.082 |
2.500 |
2.918 |
3.336 |
3.754 |
Source: Railroad-Highway Grade Crossing Handbook, Second Edition. Washington, DC: U.S. Department of Transportation, Federal Highway Administration, 1986.
Table 22. U.S. DOT Final Accident Prediction from Initial Prediction and Accident History
(3 years of accident data (T = 3))
Initial Prediction from Basic Model, a |
Number of Accidents, N, in T Years |
||||||||||||
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
0.00 |
0.000 |
0.043 |
0.087 |
0.130 |
0.174 |
0.217 |
0.261 |
0.304 |
0.348 |
0.391 |
0.435 |
0.478 |
0.522 |
0.01 |
0.008 |
0.059 |
0.110 |
0.161 |
0.212 |
0.263 |
0.314 |
0.364 |
0.415 |
0.466 |
0.517 |
0.568 |
0.619 |
0.02 |
0.017 |
0.074 |
0.132 |
0.190 |
0.248 |
0.306 |
0.364 |
0.421 |
0.479 |
0.537 |
0.595 |
0.653 |
0.711 |
0.03 |
0.024 |
0.089 |
0.153 |
0.218 |
0.282 |
0.347 |
0.411 |
0.476 |
0.540 |
0.605 |
0.669 |
0.734 |
0.798 |
0.04 |
0.031 |
0.102 |
0.173 |
0.244 |
0.315 |
0.386 |
0.457 |
0.528 |
0.598 |
0.669 |
0.740 |
0.811 |
0.882 |
0.05 |
0.038 |
0.115 |
0.192 |
0.269 |
0.346 |
0.423 |
0.500 |
0.577 |
0.654 |
0.731 |
0.808 |
0.885 |
0.962 |
0.06 |
0.045 |
0.128 |
0.211 |
0.293 |
0.376 |
0.459 |
0.541 |
0.624 |
0.707 |
0.789 |
0.872 |
0.955 |
1.038 |
0.07 |
0.051 |
0.140 |
0.228 |
0.316 |
0.404 |
0.493 |
0.581 |
0.669 |
0.757 |
0.846 |
0.934 |
1.022 |
1.110 |
0.08 |
0.058 |
0.151 |
0.245 |
0.338 |
0.432 |
0.525 |
0.619 |
0.712 |
0.806 |
0.899 |
0.993 |
1.086 |
1.180 |
0.09 |
0.063 |
0.162 |
0.261 |
0.359 |
0.458 |
0.556 |
0.655 |
0.754 |
0.852 |
0.951 |
1.049 |
1.148 |
1.246 |
0.10 |
0.069 |
0.172 |
0.276 |
0.379 |
0.483 |
0.586 |
0.690 |
0.793 |
0.897 |
1.000 |
1.103 |
1.207 |
1.310 |
0.20 |
0.114 |
0.257 |
0.400 |
0.543 |
0.686 |
0.829 |
0.971 |
1.114 |
1.257 |
1.400 |
1.543 |
1.686 |
1.829 |
0.30 |
0.146 |
0.317 |
0.488 |
0.659 |
0.829 |
1.000 |
1.171 |
1.341 |
1.512 |
1.683 |
1.854 |
2.024 |
2.195 |
0.40 |
0.170 |
0.362 |
0.553 |
0.745 |
0.936 |
1.128 |
1.319 |
1.511 |
1.702 |
1.894 |
2.085 |
2.277 |
2.468 |
0.50 |
0.189 |
0.396 |
0.604 |
0.811 |
1.019 |
1.226 |
1.434 |
1.642 |
1.849 |
2.057 |
2.264 |
2.472 |
2.679 |
0.60 |
0.203 |
0.424 |
0.644 |
0.864 |
1.085 |
1.305 |
1.525 |
1.746 |
1.966 |
2.186 |
2.407 |
2.627 |
2.847 |
0.70 |
0.215 |
0.446 |
0.677 |
0.908 |
1.138 |
1.369 |
1.600 |
1.831 |
2.062 |
2.292 |
2.523 |
2.754 |
2.985 |
0.80 |
0.225 |
0.465 |
0.701 |
0.944 |
1.183 |
1.423 |
1.662 |
1.901 |
2.141 |
2.380 |
2.620 |
2.859 |
3.099 |
0.90 |
0.234 |
0.481 |
0.727 |
0.974 |
1.221 |
1.468 |
1.714 |
1.961 |
2.208 |
2.455 |
2.701 |
2.948 |
3.195 |
1.00 |
0.241 |
0.494 |
0.747 |
1.000 |
1.253 |
1.506 |
1.759 |
2.012 |
2.265 |
2.518 |
2.771 |
3.024 |
3.277 |
1.10 |
0.247 |
0.506 |
0.764 |
1.022 |
1.281 |
1.539 |
1.798 |
2.056 |
2.315 |
2.573 |
2.831 |
3.090 |
3.348 |
1.20 |
0.253 |
0.516 |
0.779 |
1.042 |
1.305 |
1.568 |
1.832 |
2.095 |
2.358 |
2.621 |
2.884 |
3.147 |
3.411 |
1.30 |
0.257 |
0.525 |
0.792 |
1.059 |
1.327 |
1.594 |
1.861 |
2.129 |
2.396 |
2.663 |
2.931 |
3.198 |
3.465 |
1.40 |
0.262 |
0.533 |
0.804 |
1.075 |
1.346 |
1.617 |
1.888 |
2.159 |
2.430 |
2.701 |
2.972 |
3.243 |
3.514 |
1.50 |
0.265 |
0.540 |
0.814 |
1.088 |
1.363 |
1.637 |
1.912 |
2.186 |
2.460 |
2.735 |
3.009 |
3.283 |
3.558 |
1.60 |
0.269 |
0.546 |
0.824 |
1.101 |
1.378 |
1.655 |
1.933 |
2.210 |
2.487 |
2.765 |
3.042 |
3.319 |
3.597 |
1.70 |
0.272 |
0.552 |
0.832 |
1.112 |
1.392 |
1.672 |
1.952 |
2.232 |
2.512 |
2.792 |
3.072 |
3.352 |
3.632 |
1.80 |
0.275 |
0.557 |
0.840 |
1.122 |
1.405 |
1.687 |
1.969 |
2.252 |
2.534 |
2.817 |
3.099 |
3.382 |
3.664 |
1.90 |
0.271 |
0.562 |
0.847 |
1.131 |
1.416 |
1.701 |
1.985 |
2.270 |
2.555 |
2.839 |
3.124 |
3.409 |
3.693 |
2.00 |
0.280 |
0.566 |
0.853 |
1.140 |
1.427 |
1.713 |
2.000 |
2.287 |
2.573 |
2.860 |
3.147 |
3.434 |
3.720 |
2.10 |
0.282 |
0.570 |
0.859 |
1.148 |
1.436 |
1.725 |
2.013 |
2.302 |
2.591 |
2.879 |
3.168 |
3.456 |
3.745 |
2.20 |
0.284 |
0.574 |
0.865 |
1.555 |
1.445 |
1.735 |
2.026 |
2.316 |
2.606 |
2.897 |
3.187 |
3.477 |
3.768 |
2.30 |
0.286 |
0.578 |
0.870 |
1.161 |
1.453 |
1.745 |
2.037 |
2.329 |
2.621 |
2.913 |
3.205 |
3.497 |
3.789 |
2.40 |
0.287 |
0.581 |
0.874 |
1.168 |
1.461 |
1.754 |
2.048 |
2.341 |
2.635 |
2.928 |
3.222 |
3.515 |
3.808 |
2.50 |
0.289 |
0.584 |
0.879 |
1.173 |
1.468 |
1.763 |
2.058 |
2.353 |
2.647 |
2.942 |
3.237 |
3.532 |
3.827 |
Source: Railroad-Highway Grade Crossing Handbook, Second Edition. Washington, DC: U.S. Department of Transportation, Federal Highway Administration, 1986.
Table 23. U.S. DOT Final Accident Prediction from Initial Prediction and Accident History
(4 years of accident data (T = 4))
Initial Prediction from Basic Model, a |
Number of Accidents, N, in T Years |
||||||||||||||
0 |
1 |
22 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
0.00 |
0.000 |
0.042 |
0.083 |
0.125 |
0.167 |
0.208 |
0.250 |
0.292 |
0.333 |
0.375 |
0.417 |
0.458 |
0.500 |
0.542 |
0.583 |
0.01 |
0.008 |
0.056 |
0.105 |
0.135 |
0.202 |
0.250 |
0.298 |
0.347 |
0.395 |
0.444 |
0.492 |
0.540 |
0.589 |
0.637 |
0.685 |
0.02 |
0.016 |
0.070 |
0.125 |
0.180 |
0.234 |
0.289 |
0.344 |
0.398 |
0.453 |
0.508 |
0.563 |
0.617 |
0.672 |
0.727 |
0.781 |
0.03 |
0.023 |
0.083 |
0.144 |
0.205 |
0.265 |
0.326 |
0.386 |
0.447 |
0.500 |
0.568 |
0.629 |
0.689 |
0.750 |
0.811 |
0.871 |
0.04 |
0.029 |
0.096 |
0.162 |
0.228 |
0.294 |
0.360 |
0.426 |
0.493 |
0.559 |
0.625 |
0.691 |
0.757 |
0.824 |
0.890 |
0.956 |
0.05 |
0.036 |
0.107 |
0.179 |
0.250 |
0.321 |
0.393 |
0.464 |
0.536 |
0.607 |
0.679 |
0.750 |
0.821 |
0.893 |
0.964 |
1.036 |
0.06 |
0.042 |
0.118 |
0.194 |
0.271 |
0.347 |
0.424 |
0.500 |
0.576 |
0.653 |
0.729 |
0.806 |
0.882 |
0.958 |
1.035 |
1.111 |
0.07 |
0.047 |
0.128 |
0.209 |
0.291 |
0.372 |
0.453 |
0.534 |
0.615 |
0.696 |
0.777 |
0.858 |
0.939 |
1.020 |
1.101 |
1.182 |
0.08 |
0.053 |
0.138 |
0.224 |
0.309 |
0.395 |
0.480 |
0.566 |
0.651 |
0.737 |
0.822 |
0.908 |
0.993 |
1.079 |
1.164 |
1.250 |
0.09 |
0.058 |
0.147 |
0.237 |
0.327 |
0.417 |
0.506 |
0.596 |
0.686 |
0.776 |
0.865 |
0.955 |
1.045 |
1.135 |
1.224 |
1.314 |
0.10 |
0.062 |
0.156 |
0.250 |
0.344 |
0.438 |
0.531 |
0.625 |
0.719 |
0.812 |
0.906 |
1.000 |
1.094 |
1.188 |
1.281 |
1.375 |
0.20 |
0.100 |
0.225 |
0.350 |
0.475 |
0.600 |
0.726 |
0.850 |
0.975 |
1.100 |
1.225 |
1.350 |
1.475 |
1.600 |
1.725 |
1.850 |
0.30 |
0.125 |
0.271 |
0.417 |
0.563 |
0.708 |
0.854 |
1.000 |
1.146 |
1.292 |
1.437 |
1.583 |
1.729 |
1.875 |
2.021 |
2.167 |
0.40 |
0.143 |
0.304 |
0.464 |
0.625 |
0.786 |
0.946 |
1.107 |
1.268 |
1.429 |
1.589 |
1.750 |
1.911 |
2.071 |
2.232 |
2.393 |
0.50 |
0.156 |
0.328 |
0.500 |
0.672 |
0.844 |
1.016 |
1.188 |
1.359 |
1.531 |
1.703 |
1.875 |
2.047 |
2.219 |
2.391 |
2.563 |
0.60 |
0.167 |
0.347 |
0.528 |
0.708 |
0.889 |
1.069 |
1.250 |
1.431 |
1.611 |
1.792 |
1.972 |
2.153 |
2.333 |
2.514 |
2.694 |
0.70 |
0.175 |
0.363 |
0.550 |
0.738 |
0.925 |
1.113 |
1.300 |
1.488 |
1.675 |
1.863 |
2.050 |
2.238 |
2.425 |
2.613 |
2.800 |
0.80 |
0.182 |
0.375 |
0.568 |
0.761 |
0.955 |
1.148 |
1.341 |
1.534 |
1.727 |
1.920 |
2.114 |
2.307 |
2.500 |
2.693 |
2.886 |
0.90 |
0.188 |
0.385 |
0.583 |
0.781 |
0.979 |
1.177 |
1.375 |
1.573 |
1.771 |
1.969 |
2.167 |
2.365 |
2.563 |
2.760 |
2.958 |
1.00 |
0.192 |
0.394 |
0.596 |
0.798 |
1.000 |
1.202 |
1.404 |
1.606 |
1.808 |
2.010 |
2.212 |
2.413 |
2.615 |
2.817 |
3.019 |
1.10 |
0.196 |
0.402 |
0.607 |
0.813 |
1.018 |
1.223 |
1.429 |
1.634 |
1.839 |
2.045 |
2.250 |
2.455 |
2.661 |
2.866 |
3.071 |
1.20 |
0.200 |
0.408 |
0.617 |
0.825 |
1.033 |
1.242 |
1.450 |
1.658 |
1.867 |
2.075 |
2.283 |
2.492 |
2.700 |
2.908 |
3.117 |
1.30 |
0.203 |
0.414 |
0.625 |
0.836 |
1.047 |
1.258 |
1.469 |
1.680 |
1.891 |
2.102 |
2.313 |
2.523 |
2.734 |
2.945 |
3.156 |
1.40 |
0.206 |
0.419 |
0.632 |
0.846 |
1.059 |
1.272 |
1.485 |
1.699 |
1.912 |
2.125 |
2.338 |
2.551 |
2.765 |
2.978 |
3.191 |
1.50 |
0.208 |
0.424 |
0.639 |
0.854 |
1.069 |
1.285 |
1.500 |
1.715 |
1.931 |
2.146 |
2.361 |
2.576 |
2.792 |
3.007 |
3.222 |
1.60 |
0.211 |
0.428 |
0.645 |
0.862 |
1.079 |
1.296 |
1.513 |
1.730 |
1.947 |
2.164 |
2.382 |
2.599 |
2.816 |
3.033 |
3.250 |
1.70 |
0.213 |
0.431 |
0.650 |
0.869 |
1.088 |
1.306 |
1.525 |
1.744 |
1.962 |
2.181 |
2.400 |
2.619 |
2.837 |
3.056 |
3.275 |
1.80 |
0.214 |
0.433 |
0.655 |
0.875 |
1.095 |
1.315 |
1.536 |
1.756 |
1.976 |
2.196 |
2.417 |
2.637 |
2.857 |
3.077 |
3.293 |
1.90 |
0.216 |
0.437 |
0.659 |
0.881 |
1.102 |
1.324 |
1.545 |
1.767 |
1.989 |
2.210 |
2.432 |
2.653 |
2.875 |
3.097 |
3.318 |
2.00 |
0.217 |
0.440 |
0.663 |
0.886 |
1.109 |
1.332 |
1.554 |
1.777 |
2.000 |
2.223 |
2.446 |
2.668 |
2.891 |
3114 |
3.337 |
2.10 |
0.219 |
0.443 |
0.667 |
0.891 |
1.115 |
1.339 |
1.562 |
1.786 |
2.010 |
2.234 |
2.458 |
2.682 |
2.906 |
3.130 |
3.354 |
2.20 |
0.220 |
0.445 |
0.670 |
0.895 |
1.120 |
1.345 |
1.570 |
1.795 |
2.020 |
2.245 |
2.470 |
2.695 |
2.920 |
3.145 |
3.370 |
2.30 |
0.221 |
0.447 |
0.673 |
0.899 |
1.125 |
1.351 |
1.577 |
1.803 |
2.029 |
2.255 |
2.481 |
2.707 |
2.933 |
3.159 |
3.385 |
2.40 |
0.222 |
0.449 |
0.676 |
0.903 |
1.130 |
1.356 |
1.583 |
1.810 |
2.037 |
2.264 |
2.491 |
2.718 |
2.944 |
3.171 |
3.398 |
2.50 |
0.223 |
0.451 |
0.679 |
0.906 |
1.134 |
1.362 |
1.589 |
1.817 |
2.045 |
2.272 |
2.500 |
2.728 |
2.955 |
3.183 |
3.411 |
Source: Railroad-Highway Grade Crossing Handbook, Second Edition. Washington, DC: U.S. Department of Transportation, Federal Highway Administration, 1986.
Table 24. U.S. DOT Final Accident Prediction from Initial Prediction and Accident History
(5 years of accident data (T = 5))
Initial Prediction from Basic Model, a |
Number of Accidents, N, in T Years |
||||||||||||||
0 |
1 |
22 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
0.00 |
0.000 |
0.040 |
0.080 |
0.120 |
0.160 |
0.200 |
0.240 |
0.280 |
0.320 |
0.360 |
0.400 |
0.440 |
0.480 |
0.560 |
|
0.01 |
0.008 |
0.054 |
0.100 |
0.146 |
0.192 |
0.238 |
0.285 |
0.331 |
0.377 |
0.423 |
0.469 |
0.515 |
0.562 |
0.654 |
|
0.02 |
0.015 |
0.067 |
0.119 |
0.170 |
0.222 |
0.274 |
0.326 |
0.378 |
0.430 |
0.481 |
0.533 |
0.585 |
0.637 |
0.741 |
|
0.03 |
0.021 |
0.079 |
0.136 |
0.193 |
0.250 |
0.307 |
0.364 |
0.421 |
0.479 |
0.536 |
0.593 |
0.650 |
0.707 |
0.821 |
|
0.04 |
0.028 |
0.090 |
0.152 |
0.214 |
0.276 |
0.338 |
0.400 |
0.462 |
0.524 |
0.586 |
0.648 |
0.710 |
0.772 |
0.897 |
|
0.05 |
0.033 |
0.100 |
0.167 |
0.233 |
0.300 |
0.367 |
0.433 |
0.500 |
0.567 |
0.633 |
0.700 |
0.767 |
0.833 |
0.967 |
|
0.06 |
0.039 |
0.110 |
0.181 |
0.252 |
0.323 |
0.394 |
0.465 |
0.535 |
0.606 |
0.677 |
0.748 |
0.819 |
0.890 |
1.032 |
|
0.07 |
0.044 |
0.119 |
0.194 |
0.269 |
0.344 |
0.419 |
0.494 |
0.569 |
0.644 |
0.719 |
0.794 |
0.869 |
0.944 |
1.094 |
|
0.08 |
0.048 |
0.127 |
0.206 |
0.285 |
0.364 |
0.442 |
0.321 |
0.600 |
0.679 |
0.758 |
0.836 |
0.915 |
0.994 |
1.152 |
|
0.09 |
0.053 |
0.135 |
0.218 |
0.300 |
0.382 |
0.465 |
0.517 |
0.629 |
0.712 |
0.794 |
0.876 |
0.959 |
1.041 |
1.206 |
|
0.10 |
0.057 |
0.143 |
0.229 |
0.314 |
0.400 |
0.486 |
0.571 |
0.657 |
0.743 |
0.829 |
0.914 |
1.000 |
1.086 |
1.257 |
|
0.20 |
0.089 |
0.200 |
0.311 |
0.422 |
0.533 |
0.644 |
0.756 |
0.867 |
0.978 |
1.089 |
1.200 |
1.311 |
1.422 |
1.644 |
|
0.30 |
0.109 |
0.236 |
0.364 |
0.491 |
0.618 |
0.745 |
0.873 |
1.000 |
1.127 |
1.255 |
1.382 |
1.509 |
1.636 |
1.891 |
|
0.40 |
0.123 |
0.262 |
0.400 |
0.538 |
0.677 |
0.815 |
0.954 |
1.092 |
1.231 |
1.369 |
1.508 |
1.646 |
1.785 |
2.062 |
|
0.50 |
0.133 |
0.280 |
0.427 |
0.573 |
0.720 |
0.867 |
1.013 |
1.160 |
1.307 |
1.453 |
1.600 |
1.747 |
1.893 |
2.187 |
|
0.60 |
0.141 |
0.294 |
0.447 |
0.600 |
0.753 |
0.906 |
1.059 |
1.212 |
1.365 |
1.518 |
1.671 |
1.824 |
1.976 |
2.282 |
|
0.70 |
0.147 |
0.305 |
0.463 |
0.621 |
0.779 |
0.937 |
1.095 |
1.253 |
1.411 |
1.568 |
1.726 |
1.884 |
2.042 |
2.358 |
|
0.80 |
0.152 |
0.314 |
0.476 |
0.638 |
0.800 |
0.962 |
1.124 |
1.286 |
1.448 |
1.610 |
1.771 |
1.933 |
2.095 |
2.419 |
|
0.90 |
0.157 |
0.322 |
0.487 |
0.652 |
0.817 |
0.983 |
1.148 |
1.313 |
1.478 |
1.643 |
1.809 |
1.974 |
2.139 |
2.470 |
|
1.00 |
0.160 |
0.328 |
0.496 |
0.664 |
0.832 |
1.000 |
1.168 |
1.336 |
1.504 |
1.672 |
1.840 |
2.008 |
2.176 |
2.512 |
|
1.10 |
0.163 |
0.333 |
0.504 |
0.674 |
0.844 |
1.015 |
1.185 |
1.356 |
1.526 |
1.696 |
1.867 |
2.037 |
2.207 |
2.548 |
|
1.20 |
0.166 |
0.338 |
0.510 |
0.683 |
0.855 |
1.028 |
1.200 |
1.372 |
1.545 |
1.717 |
1.890 |
2.062 |
2.234 |
2.579 |
|
1.30 |
0.168 |
0.342 |
0.516 |
0.690 |
0.865 |
1.039 |
1.213 |
1.387 |
1.561 |
1.735 |
1.910 |
2.084 |
2.258 |
2.606 |
|
1.40 |
0.170 |
0.345 |
0.521 |
0.697 |
0.873 |
1.048 |
1.224 |
1.400 |
1.576 |
1.752 |
1.927 |
2.103 |
2.279 |
2.630 |
|
1.50 |
0.171 |
0.349 |
0. 526 |
0.703 |
0.880 |
1.057 |
1.234 |
1.411 |
1.589 |
1.766 |
1.943 |
2.120 |
2.297 |
2.651 |
|
1.60 |
0.173 |
0.351 |
0.530 |
0.708 |
0.886 |
1.065 |
1.243 |
1.422 |
1.600 |
1.779 |
1.957 |
2.135 |
2.314 |
2.670 |
|
1.70 |
0.174 |
0.354 |
0.533 |
0.713 |
0.892 |
1.072 |
1. 251 |
1.431 |
1.610 |
1.790 |
1.969 |
2.149 |
2.328 |
2.687 |
|
1.80 |
0.176 |
0.356 |
0.537 |
0.717 |
0.898 |
1.078 |
1.259 |
1.439 |
1.620 |
1.800 |
1.980 |
2.161 |
2.341 |
2.702 |
|
1.90 |
0.177 |
0.358 |
0.540 |
0.721 |
0.902 |
1.084 |
1.265 |
1.447 |
1.628 |
1.809 |
1.991 |
2.172 |
2.353 |
2.716 |
|
2.00 |
0.178 |
0.360 |
0.542 |
0.724 |
0.907 |
1.089 |
1.271 |
1.453 |
1.636 |
1.818 |
2.000 |
2.182 |
2.364 |
2.729 |
|
2.10 |
0.179 |
0.362 |
0.545 |
0.728 |
0.911 |
1.094 |
1.277 |
1.460 |
1.643 |
1.826 |
2.009 |
2.191 |
2.374 |
2.740 |
|
2.20 |
0.180 |
0.363 |
0.547 |
0.731 |
0.914 |
1.098 |
1.282 |
1.465 |
1.649 |
1.833 |
2.016 |
2.200 |
2.384 |
2.751 |
|
2.30 |
0.180 |
0.365 |
0.549 |
0.733 |
0.918 |
1.102 |
1.286 |
1.471 |
1.655 |
1.839 |
2.024 |
2.208 |
2.392 |
2.761 |
|
2.40 |
0.181 |
0.366 |
0.551 |
0.736 |
0.921 |
1.106 |
1.291 |
1.475 |
1.660 |
1.845 |
2.030 |
2.215 |
2.400 |
2.770 |
|
2.50 |
0.182 |
0.367 |
0.553 |
0.738 |
0.924 |
1.109 |
1.295 |
1.480 |
1.665 |
1.851 |
2.036 |
2.222 |
2.407 |
2.778 |
|
Source: Railroad-Highway Grade Crossing Handbook, Second Edition. Washington, DC: U.S. Department of Transportation, Federal Highway Administration, 1986.
The probability of an injury accident given an accident is:
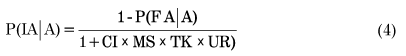
where:
P(FA|A) = probability of a fatal accident, given an accident
CI = formula constant = 4.280
MS = factor for maximum timetable train speed
TK = factor for number of tracks
UR = factor for urban or rural crossing
The equations for calculating values of the factors are listed in Table 25 for the fatal accident probability formula and Table 26 for the injury accident probability formula. To simplify use of the formulae, the values of the factors have been tabulated for typical values of crossing characteristics and are given in Tables 27 and 28 for the fatal accident and injury accident probability formulae, respectively.
Table 25. Equations for Crossing Characteristic Factors for U.S. DOT Fatal Accident Probability Formula
Fatal Accident Probability Formula:
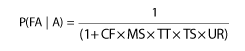
Crossing Characteristic Factor |
Equation for Crossing Characteristic Factor |
Formula constant |
CF = 695 |
Maximum timetable train speed factor |
MS = ms-1.074 |
Thru trains per day |
TT = (tt + 1)-0.1025 |
Switch train per day factor |
TS = (tt + 1)0.1025 |
Urban-Rural crossing factor |
UR = e0.1880ur |
where: ms = maximum timetable train speed, mph
tt = number of thru trains per day
ts = number of switch trains per day
ur = 1, urban crossing
= 0, rural crossing
Source: Railroad-Highway Grade Crossing Handbook, Second Edition. Washington, DC: U.S. Department of Transportation, Federal Highway Administration, 1986.
Table 26. Equations for Crossing Characteristic Factors for U.S. DOT Injury Accident Probability Formula
Injury Accident Probability Formula:
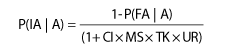
Crossing Characteristic Factor |
Equation for Crossing Characteristic Factor |
Fatal accident probability |
P(FA|A) - See Table 25 |
Formula constant |
CI = 4.280 |
Maximum timetable train speed factor |
MS = ma-02334 |
Number of tracks factor |
TK = e01176tk |
Urban-Rural crossing factor |
UR = e01844ur |
where: ms = maximum timetable train speed, mph
tk = total number of tracks at crossing
ur = 1, urban crossing
0, rural crossing
Source: Railroad-Highway Grade Crossing Handbook, Second Edition. Washington, DC: U.S. Department of Transportation, Federal Highway Administration, 1986.
Table 27. Factor Values for U.S. DOT Fatal Accident Probability Formula
Fatal Accident Probability Formula:
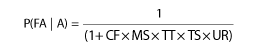
where: CF = 695.0, formula constant
UR = 1.207, urban crossing
= 1.000, rural crossing, and
Maximum |
MS |
Thru |
TT |
Switch |
TS |
1 |
1.000 |
0 |
1.000 |
0 |
1.000 |
5 |
0.178 |
1 |
0.931 |
1 |
1.074 |
10 |
0.084 |
2 |
0.894 |
2 |
1.119 |
15 |
0.055 |
3 |
0.868 |
3 |
1.152 |
20 |
0.040 |
4 |
0.848 |
4 |
1.179 |
25 |
0.032 |
5 |
0.832 |
5 |
1.202 |
30 |
0.026 |
6 |
0.819 |
6 |
2.221 |
40 |
0.019 |
7 |
0.808 |
7 |
1.238 |
50 |
0.015 |
9 |
0.790 |
9 |
1.266 |
60 |
0.012 |
10 |
0.782 |
10 |
1.279 |
70 |
0.010 |
20 |
0.732 |
20 |
1.366 |
80 |
0.009 |
30 |
0.703 |
30 |
1.422 |
90 |
0.008 |
40 |
0.683 |
40 |
1.464 |
100 |
0.007 |
50 |
0.668 |
50 |
1.497 |
Source: Railroad-Highway Grade Crossing Handbook, Second Edition. Washington, DC: U.S. Department of Transportation, Federal Highway Administration, 1986.
Table 28. Factor Values for U.S. DOT Injury Accident Probability Formula
Injury Accident Probability Formula:
![]()
where: P(FA|A) = Fatal accident probability, See Tables 25 and 27
CI = 4.280, formula constant
UR = 1.202, urban crossing
= 1.000, rural crossing, and
Maximum |
MS |
Total |
TK |
1 |
1.000 |
0 |
1.000 |
5 |
0.687 |
1 |
1.125 |
10 |
0.584 |
2 |
1.265 |
15 |
0.531 |
3 |
1.423 |
20 |
0.497 |
5 |
1.800 |
25 |
0.472 |
6 |
2.025 |
30 |
0.452 |
7 |
2.278 |
40 |
0.423 |
8 |
2.562 |
50 |
0.401 |
9 |
2.882 |
60 |
0.385 |
10 |
3.241 |
70 |
0.371 |
15 |
5.836 |
80 |
0.360 |
20 |
10.507 |
90 |
0.350 |
||
100 |
0.341 |
Source: Railroad-Highway Grade Crossing Handbook, Second Edition. Washington, DC: U.S. Department of Transportation, Federal Highway Administration, 1986.
* Includes previously unpublished materials provided by Ray Lewis, West Virginia Department of Transportation, 2006.
Federal requirements dictate that each state shall establish priorities for its crossing program based on:
• The potential reduction in collisions or collision severities.
• The project costs and available resources.
• The relative hazard of each crossing based on a hazard index formula.
• An on-site inspection of each candidate crossing.
• The potential danger to large numbers of people at crossings used on a regular basis by passenger trains or buses or by trains or motor vehicles carrying hazardous materials.
• Other criteria as deemed appropriate by each state.57
Engineering studies should be conducted of highway-rail crossings that have been selected from the priority list. The purpose of these studies is to:
• Review the crossing and its environment.
• Identify the nature of any problems.
• Recommend alternative improvements.
An engineering study consists of a review of site characteristics, the existing traffic control system, and highway and railroad operational characteristics. Based on a review of these conditions, an assessment of existing and potential hazards can be made. If safety deficiencies are identified, countermeasures can be recommended.
1. Diagnostic Team Study Method
The procedure recommended in earlier editions of this handbook, adopted in FHWA’s Highway Safety Engineering Study Procedural Guide,58 and adopted in concept by several states is the diagnostic team study approach. This term is used to describe a simple survey procedure utilizing experienced individuals from several sources. The procedure involves the diagnostic team’s evaluation of the crossing as to its deficiencies and judgmental consensus as to the recommended improvements.
The primary factors to be considered when assigning people to the diagnostic team are that the team is interdisciplinary and representative of all groups having responsibility for the safe operation of crossings so that each of the vital factors relating to the operational and physical characteristics of the crossing may be properly identified. Individual team members are selected on the basis of their specific expertise and experience. The overall structure of the team is built upon three desired areas of responsibility:
• Local responsibility.
• Administrative responsibility.
• Advisory capability.
For the purpose of the diagnostic team, the operational and physical characteristics of crossings can be classified into three areas:
Traffic operations. This area includes both vehicular and train traffic operation. The responsibilities of highway traffic engineers and railroad operating personnel chosen for team membership include, among other criteria, specific knowledge of highway and railroad safety, types of vehicles and trains, and their volumes and speeds.
Traffic control devices. Highway maintenance engineers, signal control engineers, and railroad signal engineers provide the best source for expertise in this area. Responsibilities of these team members include knowledge of active traffic control systems, interconnection with adjacent signalized highway intersections, traffic control devices for vehicle operations in general and at crossings, and crossing signs and pavement markings.
Administration. It is necessary to realize that many of the problems relating to crossing safety involve the apportionment of administrative and financial responsibility. This should be reflected in the membership of the diagnostic team. The primary responsibility of these members is to advise the team of specific policy and administrative rules applicable to the modification of crossing traffic control devices.
To ensure appropriate representation on the diagnostic team, it is suggested that the team comprise at least a traffic engineer with safety experience and a railroad signal engineer. Following are other disciplines that might be represented on the diagnostic team:
• Railroad administrative official.
• Highway administrative official.
• Human factors engineer.
• Law enforcement officer.
• Regulatory agency official.
• Railroad operating official.
The diagnostic team should study all available data and inspect the crossing and its surroundings with the objective of determining the conditions that affect safety and traffic operations. In conducting the study, a questionnaire is recommended to provide a structured account of the crossing characteristics and their effect on safety. Some states are now using automated diagnostic review forms to facilitate the collection, storage, and analysis of crossing data. Example forms developed and used by various states are reproduced in Appendix G. Figure 6 shows a sample questionnaire, which can be altered to fit individual agency needs. The questionnaire shown in Figure 6 is divided into four sections:
• Distant approach and advance warning.
• Immediate highway approach.
• Crossing proper.
• Summary and analysis.
To conduct the diagnostic team field study, traffic cones are placed on the approaches, as shown in Figure 7.
Crossing approach zone. Cone A is placed at the point where the driver first obtains information that there is a crossing ahead. This distance is also the beginning of the approach zone. Usually, this information comes from the advance warning sign, the pavement markings, or the crossing itself. The distance from the crossing is based on the decision sight distance, which is the distance required for a driver to detect a crossing and to formulate actions needed to avoid colliding with trains.
Tables 29 and 30 provide a range of distances from point A to the crossing stop line, dependent upon design vehicle speeds. The maximum distances are applicable to crossings with a high level of complexity and will generally be applicable on urban roads and streets. These distances correspond to the decision sight distances for stops on rural roads and for stops on urban roads in the American Association of State Highway and Transportation Officials (AASHTO) “Green Book.” In calculating sight distances, the height of the driver’s eye is considered 1.080 meter (3.5 feet) above the roadway surface for passenger vehicles; the target height is considered 0.6 meter (2.0 feet) above the roadway surface.59
Table 29. Distances in Meters to Establish Study Positions for Diagnostic Team Evaluation
Design |
Distance from |
Distance from |
50 |
155 |
70 |
60 |
195 |
95 |
70 |
235 |
115 |
80 |
280 |
140 |
90 |
325 |
170 |
100 |
370 |
200 |
110 |
420 |
235 |
120 |
470 |
265 |
* Note: The distance from the stop line is assumed to be 4.5 meters from nearest rail, or 2.4 meters from the gate if one is present.
Source: From A Policy on Geometric Design of Highway and Streets, 2004, by the American Association of State Highway and Transportation Officials, Washington, DC. Used by permission.
Figure 6. Sample Questionnaire for Diagnostic Team Evaluation
LOCATIONAL DATA: Street Name: _____________________________________ City: _____________________________________
Railroad: _________________________________________ Crossing Number: ________________________
VEHICLE DATA: No. of Approach Lanes: ______________ Approach Speed Limit: _______________ AADT: ____________
Approach Curvature: ____________________________ Approach Gradient:
TRAIN DATA: No. of Tracks: _______________ Train Speed Limit: ______________ Trains Per Day: ____________________
Track Gradients: ____________________________________________________________________________________
SECTION I—Distance Approach and Advance Warning
1. Is advance warning of railroad crossing available? If so, what devices are used? ______________________
2. Do advance warning devices alert drivers to the presence of the crossing and allow time to react to approaching train traffic?
3. Do approach grades, roadway curvature, or obstructions limit the view of advance warning devices? ___ If so, how?
4. Are advance warning devices readable under night, rainy, snowy, or foggy conditions? ______________________
SECTION II—Immediate Highway Approach
1. What maximum safe approach speed will existing sight distance support? ________________________________
2. Is that speed equal to or above the speed limit on that part of the highway? _______________________________
3. If not, what has been done, or reasonably could be done, to bring this to the driver’s attention? _______________
4. What restrictive obstructions to sight distance might be removed? ___________________________________________
5. Do approach grades or roadway curvature restrict the driver’s view of the crossing? ________________________
6. Are railroad crossing signals or other active warning devices operating properly and visible to adequately warn drivers of approaching trains? __________________________________________________________________________________
SECTION III—Crossing Proper
1. From a vehicle stopped at the crossing, is the sight distance down the track to an approaching train adequate for the driver to cross the tracks safely? _______________________________________________________________________________
2. Are nearby intersection traffic signals or other control device affecting the crossing operation? If so, how?
3. Is the stopping area at the crossing adequately marked? ______________________________________________
4. Do vehicles required by law to stop at all crossings present a hazard at the crossing? _____ Why? ____________
5. Do conditions at the crossing contribute to, or are they conducive to, a vehicle stalling at or on the crossing?
6. Are nearby signs, crossing signals, etc. adequately protected to minimize hazards to approaching traffic? _______
7. Is the crossing surface satisfactory? ______ If not, how and why? ______________________________________
8. Is surface of highway approaches satisfactory? ___________________________________________ If not, why?
SECTION IV—Summary and Analysis
1. List major attributes of the crossing which may contribute to safety. _____________________________________
2. List features which reduce crossing safety. _______________________________________________________
3. Possible methods for improving safety at the crossing: ______________________________________________
4. Overall evaluation of crossing: _________________________________________________________________
5. Other comments: ____________________________________________________________________________
Source: Railroad-Highway Grade Crossing Handbook, Second Edition. Washington, DC: U.S. Department of Transportation, Federal Highway Administration, 1986.
Figure 7. Study Positions for Diagnostic Team
Source: Railroad-Highway Grade Crossing Handbook, Second Edition. Washington, DC: U.S. Department of Transportation, Federal Highway Administration, 1986.
Table 30. Distances in Feet to Establish Study Positions for Diagnostic Team Evaluation
Design |
Distance from |
Distance from |
30 |
490 |
220 |
40 |
690 |
330 |
50 |
910 |
465 |
55 |
1030 |
535 |
60 |
1150 |
610 |
70 |
1410 |
780 |
* Note: The distance from the stop line is assumed to be 15 feet from nearest rail, or 8 feet from the gate if one is present.
Source: From A Policy on Geometric Design of Highway and Streets, 2004, by the American Association of State Highway and Transportation Officials, Washington, DC. Used by permission.
Safe stopping point. Cone B is placed at the point where the approaching driver must be able to see an approaching train so that a safe stop can be made if necessary. This point is located at the end of the approach zone and the end of the non-recovery zone. Distances to point B are based on the design vehicle speed and are also shown in Tables 29 and 30. These distances are stopping sight distances to the stop line and are in accordance with the upper end of the range of stopping sight distances in the AASHTO “Green Book.”60 In calculating these distances, a level approach is assumed. If this is not the case, an allowance must be made for the effects of positive or negative approach grades.
Stop line. Cone C is placed at the stop line, which is assumed to be 4.6 meters (15 feet) from the near rail of the crossing, or 8 feet from the gate if one is present.
The questions in Section I of the questionnaire (refer to Figure 6) are concerned with the following:
• Driver awareness of the crossing.
• Visibility of the crossing.
• Effectiveness of advance warning signs and signals.
• Geometric features of the highway.
When responding to questions in this section, the crossing should be observed from the beginning of the approach zone, at traffic cone A.
The questions in Section II (refer to Figure 6) are concerned with whether the driver has sufficient information to detect an approaching train and make correct decisions about crossing safely. Observations for responding to questions in this section should be made from cone B. Factors considered by these questions include the following:
• Driver awareness of approaching trains.
• Driver dependence on crossing signals.
• Obstruction of view of train’s approach.
• Roadway geometrics diverting driver attention.
• Potential location of standing railroad cars.
• Possibility of removal of sight obstructions.
• Availability of information for stop or go decision by the driver.
The questions in Section III (refer to Figure 6) apply to observations adjacent to the crossing, at cone C. Of particular concern, especially when the driver must stop, is the ability to see down the tracks for approaching trains. Intersecting streets and driveways should also be observed to determine whether intersecting traffic could affect the operation of highway vehicles over the crossing. Questions in this section relate to the following:
• Sight distance down the tracks.
• Pavement markings.
• Conditions conducive to vehicles becoming stalled or stopped on the crossing.
• Operation of vehicles required by law to stop at the crossing.
• Signs and signals as fixed object hazards.
• Opportunity for evasive action by the driver.
Corner sight distance.61 Available sight distances help determine the safe speed at which a vehicle can approach a crossing. The following three sight distances should be considered:
• Distance ahead to the crossing.
• Distance to and along the tracks on which a train might be approaching the crossing from either direction.
• Sight distance along the tracks in either direction from a vehicle stopped at the crossing.
These sight distances are illustrated in Figure 8.
In the first case, the distance ahead to the crossing, the driver must determine whether a train is occupying the crossing or whether there is an active traffic control device indicating the approach or presence of a train. In such an event, the vehicle must be stopped short of the crossing, and the available sight distance may be a determining factor limiting the speed of an approaching vehicle.
The relationship between vehicle speed and this sight distance is set forth in the following formula:
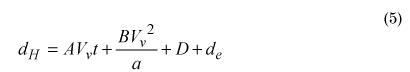
where:
dH = sight distance measured along the highway from the nearest rail to the driver of a vehicle, which allows the vehicle to be safely stopped without encroachment of the crossing area, feet
A = constant = 1.47
B = constant = 1.075
Vv = velocity of the vehicle, miles per hour (mph)
t = perception-reaction time, seconds, assumed to be 2.5 seconds
a = driver deceleration, assumed to be 11.2 feet per second2
D = distance from the stop line or front of vehicle to the near rail, assumed to be 15 feet
de = distance from the driver to the front of the vehicle, assumed to be 8 feet
This formula is also expressed in SI Metric terms, as follows:
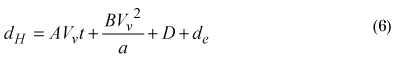
where:
dH = sight distance measured along the highway from the nearest rail to the driver of a vehicle, which allows the vehicle to be safely stopped without encroachment of the crossing area, feet
A = constant = 0.278
B = constant = 0.039
V = velocity of the vehicle, kilometers per hour (km/ hr.)
t = perception-reaction time, seconds, assumed to be 2.5 seconds
a = driver deceleration, assumed to be 3.4 meters per second2
D = distance from the stop line or front of vehicle to the near rail, assumed to be 4.5 meters
de = distance from the driver to the front of the vehicle, assumed to be 2.4 meters
The minimum safe sight distances, dH, along the highway for selected vehicle speeds are shown in the bottom line of Tables 31 and 32. As noted, these distances were calculated for certain assumed conditions and should be increased for less favorable conditions.
The second sight distance utilizes a so-called “sight triangle” in the quadrants on the vehicle approach side of the track. This triangle is formed by:
• The distance (dH) of the vehicle driver from the track.
• The distance (dt) of the train from the crossing.
• The unobstructed sight line from the driver to the front of the train.
This sight triangle is depicted in Figure 8. The relationships between vehicle speed, maximum timetable train speed, distance along the highway (dH), and distance along the railroad are set forth in the following formula:
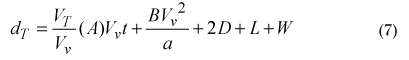
Figure 8. Crossing Sight Distances
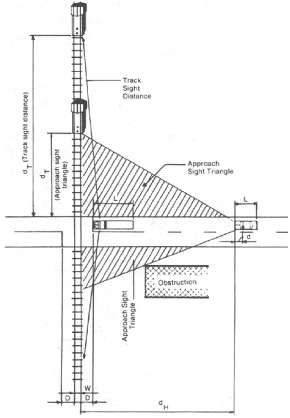
Source: Railroad-Highway Grade Crossing Handbook, Second Edition. Washington, DC: U.S. Department of Transportation, Federal Highway Administration, 1986.
where:
dT = sight distance along the railroad tracks to permit the vehicle to cross and be clear of the crossing upon arrival of the train
A = constant = 1.47
B = constant = 1.075
Vv = velocity of the vehicle, mph
t = perception-reaction time, seconds, assumed to be 2.5 seconds
a = driver deceleration, assumed to be 11.2 feet per second2
D = distance from the stop line or front of vehicle to the near rail, assumed to be 15 feet
L = length of vehicle, assumed to be 65 feet
W = distance between outer rails (for a single track, this value is 5 feet)
In SI Metric values, this formula becomes:
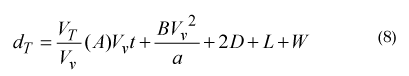
where:
dT = sight distance along the railroad tracks to permit the vehicle to cross and be clear of the crossing upon arrival of the train
A = constant = 0.278
B = constant = 0.039
Vv = velocity of the vehicle, km/hr.
t = perception-reaction time, seconds, assumed to be 2.5 seconds a = driver deceleration, assumed to be 3.4 meters per second2
D = distance from the stop line or front of vehicle to the near rail, assumed to be 4.5 meters L = length of vehicle, assumed to be 20 meters
W = distance between outer rails (for a single track,this value is 1.5 meters)
Distances dh and dT are shown in Tables 31 and 32 for several selected highway speeds and train speeds.
Clearing sight distance. In the case of a vehicle stopped at a crossing, the driver needs to see both ways along the track to determine whether a train is approaching and to estimate its speed. The driver needs to have a sight distance along the tracks that will permit sufficient time to accelerate and clear the crossing prior to the arrival of a train, even though the train might come into view as the vehicle is beginning its departure process.
Figure 9 illustrates the maneuver. These sight distances, for a range of train speeds, are given in the column for a vehicle speed of zero in Tables 31 and 32. These values are obtained from the following formula:
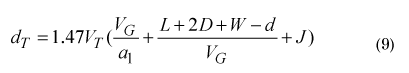
where:
VG = maximum speed of vehicle in selected starting gear, assumed to be 8.8 feet per second
a1 = acceleration of vehicle in starting gear, assumed to be 1.47 feet per second per second
J = sum of the perception time and the time required to activate the clutch or an automatic shift, assumed to be 2 seconds
da = distance the vehicle travels while accelerating to maximum speed in first gear, or
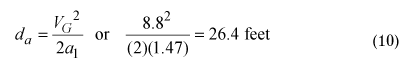
dT, VT, L, D, and W are defined as above.
Expressing the formula again in SI Metric terms:
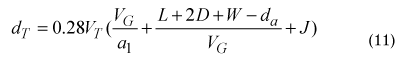
where:
VG = maximum speed of vehicle in selected starting gear, assumed to be 2.7 meters per second
a1 = acceleration of vehicle in starting gear, assumed to be 0.45 meter per second per second
J = sum of the perception time and the time required to activate the clutch or an automatic shift, assumed to be 2 seconds
da = distance the vehicle travels while accelerating to maximum speed in first gear, or
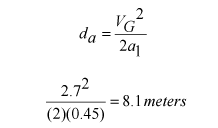
dT, VT, L, D, and W are defined as above.62
Figure 9. Sight Distance for a Vehicle Stopped at Crossing
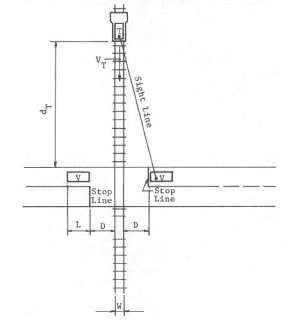
Source: Railroad-Highway Grade Crossing Handbook, Second Edition. Washington, DC: U.S. Department of Transportation, Federal Highway Administration, 1986.
Table 31. Sight Distances for Combinations of Highway Vehicle and Train Speeds, Metric
Case B: |
Case A: Moving vehicle |
|||||||||||||
Vehicle speed (km/hr.) |
||||||||||||||
Train speed (km/hr.) |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
130 |
Distance along railroad from crossing, dT (feet) |
||||||||||||||
10 |
45 |
39 |
24 |
21 |
19 |
19 |
19 |
19 |
20 |
21 |
21 |
22 |
23 |
24 |
20 |
91 |
77 |
49 |
41 |
38 |
38 |
38 |
39 |
40 |
41 |
43 |
45 |
47 |
48 |
30 |
136 |
116 |
73 |
62 |
57 |
56 |
57 |
58 |
60 |
62 |
64 |
67 |
70 |
73 |
40 |
181 |
154 |
98 |
82 |
77 |
75 |
76 |
77 |
80 |
83 |
86 |
89 |
93 |
97 |
50 |
227 |
193 |
122 |
103 |
96 |
94 |
95 |
97 |
100 |
103 |
107 |
112 |
116 |
121 |
60 |
272 |
232 |
147 |
123 |
115 |
113 |
113 |
116 |
120 |
124 |
129 |
134 |
140 |
145 |
70 |
317 |
270 |
171 |
144 |
134 |
131 |
132 |
135 |
140 |
145 |
150 |
156 |
163 |
169 |
80 |
362 |
309 |
196 |
164 |
153 |
150 |
151 |
155 |
160 |
165 |
172 |
179 |
186 |
194 |
90 |
408 |
347 |
220 |
185 |
172 |
169 |
170 |
174 |
179 |
186 |
193 |
201 |
209 |
218 |
100 |
453 |
386 |
245 |
206 |
192 |
188 |
189 |
193 |
199 |
207 |
215 |
223 |
233 |
242 |
110 |
498 |
425 |
269 |
226 |
211 |
207 |
208 |
213 |
219 |
227 |
236 |
246 |
256 |
266 |
120 |
544 |
463 |
294 |
247 |
230 |
225 |
227 |
232 |
239 |
248 |
258 |
268 |
279 |
290 |
130 |
589 |
502 |
318 |
267 |
249 |
244 |
246 |
251 |
259 |
269 |
279 |
290 |
302 |
315 |
140 |
634 |
540 |
343 |
288 |
268 |
263 |
265 |
271 |
279 |
289 |
301 |
313 |
326 |
339 |
Distance along highway from crossing, dH (feet) |
||||||||||||||
15 |
25 |
38 |
53 |
70 |
90 |
112 |
136 |
162 |
191 |
222 |
255 |
291 |
||
Source: From A Policy on Geometric Design of Highway and Streets, 2004, by the American Association of State Highway and Transportation Officials, Washington, DC. Used by permission.
Table 32. Sight Distances for Combinations of Highway Vehicle and Train Speeds, U.S. Customary
Case B: Departure from stop |
Case A: Moving vehicle |
||||||||
Vehicle speed (mph) |
|||||||||
Train speed (mph) |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
Distance along railroad from crossing, dT (feet) |
|||||||||
10 |
240 |
146 |
106 |
99 |
100 |
105 |
111 |
118 |
126 |
20 |
480 |
293 |
212 |
198 |
200 |
209 |
222 |
236 |
252 |
30 |
721 |
439 |
318 |
297 |
300 |
314 |
333 |
355 |
378 |
40 |
961 |
585 |
424 |
396 |
401 |
419 |
444 |
473 |
504 |
50 |
1201 |
732 |
530 |
494 |
501 |
524 |
555 |
591 |
630 |
60 |
1441 |
878 |
636 |
593 |
601 |
628 |
666 |
709 |
756 |
70 |
1681 |
1024 |
742 |
692 |
701 |
733 |
777 |
828 |
882 |
80 |
1921 |
1171 |
848 |
791 |
801 |
833 |
888 |
946 |
1008 |
90 |
2162 |
1317 |
954 |
890 |
901 |
943 |
999 |
1064 |
1134 |
Distance along highway from crossing, dH (feet) |
|||||||||
69 |
135 | 220 | 324 | 447 |
589 |
751 |
931 |
|||||
Source: From A Policy on Geometric Design of Highway and Streets, 2004, by the American Association of State Highway and Transportation Officials, Washington, DC. Used by permission.
Adjustments for longer vehicle lengths, slower acceleration capabilities, multiple tracks, skewed crossings, and other than flat highway grades are necessary. The formulas in this section may be used with proper adjustments to the appropriate dimensional values. It would be desirable that sight distances permit operation at the legal approach speed for highways. This is often impractical.
In Section IV of the questionnaire, the diagnostic team is given the opportunity to do the following:
• List major features that contribute to safety.
• List features that reduce crossing safety.
• Suggest methods for improving safety at the crossing.
• Give an overall evaluation of the crossing.
• Provide comments and suggestions relative to the questionnaire.
In addition to completing the questionnaire, team members should take photographs of the crossing from both the highway and the railroad approaches.
Current and projected vehicle and train operation data should be obtained from the team members. Information on the use of the crossing by buses, school buses, trucks transporting hazardous materials, and passenger trains should be provided. The evaluation of the crossing should include a thorough evaluation of collision frequency, collision types, and collision circumstances. Both train-vehicle collisions and vehicle-vehicle collisions should be examined.
Team members should drive each approach several times to become familiar with all conditions that exist at or near the crossing. All traffic control devices (signs, signals, markings, and train detection circuits) should be examined as part of this evaluation. If the crossing is equipped with signals, the railroad signal engineer should activate them so that their alignment and light intensity may be observed.
The Manual on Uniform Traffic Control Devices (MUTCD) should be a principal reference for this evaluation.63 Also, A User’s Guide to Positive Guidance provides information for conducting evaluations of traffic control devices.64
After the questionnaire has been completed, the team is reassembled for a short critique and discussion period. Each member should summarize his or her observations pertaining to safety and operations at the crossing. Possible improvements to the crossing may include the following:
• Closing of crossing—available alternate routes for highway traffic.
• Site improvements—removal of obstructions in the sight triangle, highway realignment, improved cross section, drainage, or illumination.
• Crossing surfaces—rehabilitation of the highway structure, the track structure, or both; installation of drainage and subgrade filter fabric; adjustments to highway approaches; and removal of retired tracks from the crossing.
• Traffic control devices—installation of passive or active control devices and improvement of train detection equipment.
The results and recommendations of the diagnostic team should be documented. Recommendations should be presented promptly to programming and implementation authorities.
Both government and railroad resources are becoming more limited. The Highway Safety Engineering Studies Procedural Guide suggests crossing evaluation by an individual, in lieu of the diagnostic team.65 The guide suggests that this individual be a traffic engineer with experience in highway-rail crossing and traffic safety. A background in signal control and safety program administration would also be advantageous.
2. Traffic Conflict Technique
Highway traffic collisions are a statistically rare event. Typically, an engineer or analyst must assemble several years of collision data to have a large enough sample to identify a pattern of collisions and suggest countermeasures. The traffic conflict technique was developed during the early 1970s by Research Laboratories, General Motors Corporation, to be a measure of traffic collision potential.
A traffic conflict occurs when a driver takes evasive action, brakes, or weaves to avoid a collision. The conflict is evidenced by a brake-light indication or a lane change by the offended driver. Procedures have been developed to define and record traffic conflicts to permit the performance of formal surveys.66
Originally, traffic conflict surveys had to be carried out by a team of observers in the field. The availability of inexpensive and reliable video equipment permits photographic data collection in the field, followed by more accurate and complete data analysis in the office.
3. Collision Study
Vehicle-train collisions are very infrequent at most crossings. Based on 1995 data, the average public crossing would experience a train-involved collision every 56.3 years.67 As a result, traditional collision analyses techniques are usually of limited utility.
Collision studies may be needed under the following circumstances:
• Some high-exposure crossings may experience sufficient collisions that a pattern can be established.
• It may be necessary to do an in-depth investigation of an individual collision, either as part of a safety evaluation or in preparation for litigation. See Chapter XIII for more information.
• NTSB frequently carries out in-depth studies of certain collisions or of a number of collisions that fit a certain category. NTSB’s findings and recommendations may be useful at the individual crossing level or as input to a grade crossing improvement program.
• Traditional collision study methods may be applicable to vehicle-vehicle collisions that are associated with the physical characteristics or the operation of a highway-rail grade crossing.
4. Traffic Study
Important considerations when studying traffic flow and operations at a highway-rail grade crossing are traffic volumes (daily and peak hour); speeds; the mix of vehicle types; intersecting volumes and turning movements at intersections near the crossing; the capacity of the road; delays; and the formation of any traffic queues. These should be reviewed in light of current conditions and how they might be affected by changes at the crossing.
Particular concerns are routing and access for emergency vehicles and the use of the crossing by special vehicles such as low clearance vehicles, buses, and trucks transporting hazardous materials.
If a crossing consolidation is contemplated, the effects on traffic circulation and the impact on the operation of adjacent intersections should be considered. Frequently, the consolidation of crossings also leads to the consolidation of traffic on other facilities and may permit the construction of a traffic signal at a nearby intersection or other improvements that could not be justified otherwise.
The traffic study should also consider the impacts of crossing operations on the community. Considerations include frequency and length of train operations, pedestrian and bicycle access, and the need for crossings to provide adequate access to schools and services.
Standard data collection procedures can be found in several sources, including the Highway Safety Engineering Studies Procedural Guide or the Manual of Transportation Engineering Studies from the Institute of Transportation Engineers.68, 69
5. Near-Hit Reports
Some railroads operate a program under which train crews report “near hits” with or violations by highway vehicles at crossings. These reports can be a valuable source of information regarding problem crossings and will also contain data regarding vehicle ownerships and types, time of day, and other contributing factors.
Where the vehicle can be positively identified, the reports are frequently turned over to the property protection department of the railroad (railroad police) for follow-up. This is particularly true in the case of documented violations by drivers for commercial carriers or for transit and school bus operators.
6. Enforcement Study
An enforcement study is directed at providing an objective measurement of the frequency of violations of traffic control devices and traffic laws. Hidden observers or cameras are used to observe the location or condition under study. Data collected will include total traffic volume, total vehicles encountering the situation under study, and total observed violations
The enforcement study must be carried out so that traffic operations and driver behavior are not affected. If an actual law enforcement officer or police car appears on the scene, the study should be interrupted or terminated. The measurements obtained may be used as a basis for later enforcement campaigns and may also be used to justify improvements in traffic control devices, such as the installation of constant warning time devices to improve the credibility of crossing signals.
Various types of specialized photographic equipment are available for conducting enforcement studies or for actual photographic enforcement of traffic laws. Photographic enforcement has been used successfully at grade crossings and along at least one light-rail transit corridor.70
The procedures for evaluating highway-rail grade crossings are generally based upon the physical and operational characteristics of individual crossings. A typical crossing safety program consists of a number of individual crossing projects. Funding for crossing safety is approved on the basis of the requirements of these individual projects. Therefore, crossing evaluation, programming, and construction follow traditional highway project implementation procedures.
The concept of using the systems approach to highway-rail grade crossing improvements was enhanced when crossings off the federal-aid system were made eligible for federally funded programs. Because all public crossings are now eligible for improvement with federal funds, the systems approach provides a comprehensive method for addressing safety and operations at crossings.
The systems approach considers the highway-rail grade crossing a part or a component of a larger transportation system. For this purpose, the transportation system is defined as a land surface system consisting of both highway and railroad facilities. The intersection of these two transportation modes affects both safety and operations of the entire system. The objective of the systems approach for crossings is to improve both safety and operations of the total system or segments of the system.
The systems approach may be applied to a segment of the rail component of the system. For example, to improve operating efficiency and safety over a specified segment of a rail line, all crossings would be considered in the evaluation. Thus, the systems approach is often called the corridor approach.
The systems approach may be applied to an urban area, city, or community. In this case, all public crossings within the jurisdiction of a public agency are evaluated and programmed for improvements. The desired outcome is a combination of engineering improvements and closures such that both safety and operations are highly improved.
Assume that a segment of rail line is to be upgraded for unit train operations or high-speed passenger service. This type of change in rail operations would provide an ideal opportunity for the application of the systems approach. The rail line may be upgraded by track and signal improvements for train operations that might cause a need for adjustments in train detection circuits of active traffic control devices. Also, modifications of train operations and speeds may require the installation of active traffic control devices at selected crossings.
A systems approach developed for crossings in a specified community or political subdivision allows for a comprehensive analysis of highway traffic operations. Thus, unnecessary crossings can be closed, and improvements can be made at other crossings. This approach enhances the acceptability of crossing closures by local officials and citizens.
Initially, all crossings in the system, both public and private, should be identified and classified by jurisdictional responsibility (for example, city, county, and state for public crossings; parties to the agreement for private crossings). Information should be gathered on highway traffic patterns, train operations, emergency access needs, land uses, and growth trends. Inventory records for the crossings should be updated to reflect current operational and physical characteristics. A diagnostic team consisting of representatives from all public agencies having jurisdiction over the identified crossings and the railroads operating over the crossings should make an on-site assessment of each crossing as described in the previous section. The diagnostic team’s recommendations should consider, among other things, crossing closure, installation of active traffic control devices, upgrading existing active devices, elimination by grade separation, surface improvements, and improvements in train detection circuits. In addition, modification of train operations near and at each crossing, removal of sight obstructions, rerouting of special vehicles and emergency vehicles, and railroad relocation should be considered.
Federal, state, and local crossing funding programs should be reviewed to identify the eligibility of each crossing improvement for public funding. Other funding sources include railroads, urban renewal funds, land development funds, and other public or private funding sources.
There are several advantages of the systems approach. A group of crossings may be improved more efficiently through the procurement of materials and equipment in quantity, thus reducing product procurement and transportation costs. Usually, only one agreement between the state, local jurisdiction, and railroad is necessary for all of the improvements. Train detection circuits may be designed as a part of the total railroad signal system rather than custom designed for each individual crossing. Electronic components, relay houses, and signal transmission equipment may be more efficiently utilized. Labor costs may be significantly reduced. Travel time of construction crews may be reduced when projects are in close proximity to each other.
Railroads benefit from the application of the systems approach in several ways. Train speeds may be increased due to safety improvements at crossings. Maintenance costs may be reduced if a sufficient number of crossings are closed. Other improvements may enhance the efficiency of rail operations.
Safety improvements are an obvious benefit to the public. Other benefits include reduced vehicular delays and better access for emergency vehicles.
One impediment to the systems approach is that most federal and state crossing safety improvement programs provide funding for safety improvements only. Also, safety improvement projects may be limited to crossings that rank high on a priority schedule. Another impediment is the involvement of multiple jurisdictions.
FHWA has endorsed the systems approach and its resultant identification of low-cost improvements to crossing safety and operations. FHWA sponsored a demonstration project that utilized the systems approach to improve crossings along a rail corridor in Illinois. To eliminate the need for project agreements with each local agency, the Illinois Commerce Commission issued a single order covering the work to be performed at nine locations. This accelerated the project and reduced labor-intensive work. FHWA and the Illinois Department of Transportation agreed that minimal plan submittals would be required of local agencies, and local agencies agreed to perform the necessary work at mutually agreed-upon lump sum prices under the supervision of Illinois Department of Transportation district representatives.
Improvements made as part of the demonstration project in Illinois included the following:
• Removal of vegetation.
• Pavement widening.
• Reconstruction of approaches.
• Installation of 12-inch lenses in crossing signals.
• Relocation of train loading areas.
• Closure of crossings.
• Removal of switch track.
• Installation of traffic control signs pertinent to crossing geometries.
The Florida Department of Transportation and other states have adopted policies incorporating the systems approach as part of their crossing safety improvement programs. The Florida Department of Transportation selects track segments on the basis of the following conditions:
• Abnormally high percentage of crossings with passive traffic control devices only.
• Freight trains carrying hazardous material in an environment that presents an unacceptable risk of a catastrophic event.
• Passenger train routes.
• Plans for increased rail traffic, especially commuter trains.
The North Carolina Department of Transportation (NCDOT) has used the systems approach often in recent years. Examples of these projects are the Sealed Corridor Program and traffic separation studies.
In the Sealed Corridor Program, NCDOT installed devices such as four-quadrant gates, longer gate arms, median separators, and new signs and pavement markings at every public crossing along the entire railway line between Charlotte and Greensboro, North Carolina. The program is planned to eventually cover the entire corridor between Charlotte and Raleigh, North Carolina. The entire corridor contains 172 public and 43 private railroad crossings.
In traffic separation studies, the NCDOT Rail Division works with communities to study how best to separate railroad and highway traffic. Engineers develop a comprehensive traffic separation study to determine which public crossings need improvements and which need to be closed. During the study phase, the engineering consultant collects traffic data for the public rail crossings in the study area. The consultants also take into account the economic impact of the potential closings.
A draft of the consultants’ recommendations is submitted to the Rail Division and the public for review and comment. The recommendations are prioritized to include near-term, mid-term, and long-term improvements. Public hearings are scheduled in each community to give residents a chance to voice opinions about the proposed recommendations. The forums also allow NCDOT to discuss the benefits of enhanced crossing safety.
In the implementation phase, NCDOT officials identify funding for the proposed enhancements (typically, 90 percent is federal funds with a 10-percent local match). The freight railroads sometimes provide additional resources.
Additional information on these and other NCDOT programs can be found on the NCDOT Safety Initiatives Website.71
Box, Paul C. and J.C. Oppenlander. Manual of Traffic Engineering Studies. Washington, DC: Institute of Transportation Engineers, 1976.
Code of Federal Regulations, Title 49, Washington, DC: Government Printing Office, published annually.
Farr, E.H. and J.S. Ritz. Accident Severity Prediction Formula for Rail-Highway Crossings. Washington, DC: Federal Highway Administration (FHWA), Federal Railroad Administration (FRA), Report FHWA-RD-83/092, July 1983.
Federal-Aid Policy Guide. Washington, DC: FHWA, updated periodically.
Federal Highway Administration Survey of Region and Division Offices, unpublished, 1984.
Goodell-Grivas, Inc. Highway Safety Engineering Studies: Procedural Guide. Washington, DC: FHWA, FHWA-TS-81220, June 1981.
Hitz, John and Mary Cross. Rail-Highway Crossing Resource Allocation Procedure User’s Guide. Washington, DC: FHWA and FRA, Report FHWA-IP-82-7, December 1982.
Manual on Uniform Traffic Control Devices, 2003 Edition. Washington, DC: FHWA, 2003.
A Policy on Geometric Design of Highway and Streets. Washington, DC: American Association of State Highway and Transportation Officials, 1984.
Post, T.J., G.J. Alexander, and H. Lunenfeld. A User’s Guide to Positive Guidance, Second Edition. Washington, DC: FHWA, Report FHWA-TO-81-1, December 1981.
Railroad/Highway Grade Crossing Accidents Involving Trucks Transporting Bulk Hazardous Materials, A Special Study. Washington, DC: National Transportation Safety Board, Report NTSB-RZM-81-2, September 1981.
Schoppert, David W. and Dan W. Hoyt. Factors Influencing Safety at Highway-Rail Grade Crossings. Washington, DC: Highway Research Board, National Cooperative Highway Research Program Report 50, 1968.
Traffic Control Devices Handbook. Washington, DC: FHWA, 1983.
Update Manual: National Railroad Highway Crossing Inventory. Washington, DC: U.S. Department of Transportation, 1976.
52 Unpublished material provided by Tom Woll, Federal Railroad Administration (FRA), Washington, DC, 2006.
53 Code of Federal Regulations, Title 49, Washington, DC: Superintendent of Documents, Government Printing Office, published annually.
54 Ibid.
55 FRA Office of Safety Website (safetydata.fra.dot.gov/ officeofsafety).
56 Ibid.
57 “Railroad Crossing Corridor Improvements.” Washington, DC: U.S. Department of Transportation (U.S. DOT), Federal Highway Administration (FHWA), Demonstration Projects Division, June 1986.
58 Highway Safety Engineering Studies Procedural Guide. Washington, DC: U.S. DOT, FHWA, November 1991.
59 A Policy on Geometric Design of Highways and Streets, 2004 Edition. Washington, DC: American Association of State Highway and Transportation Officials, 2004.
60 Ibid.
61 Ibid.
62. Footnote information unavailable.
63 Manual on Uniform Traffic Control Devices, 2003 Edition. Washington, DC: FHWA, 2003.
64 A User’s Guide to Positive Guidance. Washington, DC, U.S. DOT, FHWA, Office of Operations, June 1977.
65 Highway Safety Engineering Studies Procedural Guide. Washington, DC: U.S. DOT, FHWA, November 1991.
66 Perkins, Stuart R. GMR Traffic Conflicts Technique Procedures Manual. Research Laboratories, General Motors Corporation, Warren, Michigan, August 11, 1969.
67 Railroad Safety Statistics 2004 Annual Report. Washington, DC: U.S. DOT, FRA, November 2005.
68 Highway Safety Engineering Studies Procedural Guide. Washington, DC: U.S. DOT, FHWA, November 1991.
69 Manual of Transportation Engineering Studies. Washington, DC: Institute of Transportation Engineers, 1994.
70 Photographic Enforcement of Traffic Laws. Washington, DC: National Cooperative Highway Research Program Synthesis of Practice 219, 1995.
71 North Carolina Department of Transportation Safety Initiatives Website (www.bytrain.org/Safety/default.html).
| Table of Contents | Previous | Next |